3  Lerndemonstration zur Implementierung von digitalen Filtern auf Mikrocontrollern

Autor:in
Zugehörigkeit

Eduard Funkner

Hochschule Bremen - City University of Applied Sciences (HSB)

Veröffentlichungsdatum

28. Juli 2025

4 Abstract

Diese Bachelorarbeit behandelt die praxisnahe Implementierung biquadratischer digitaler IIR-Filter (Biquads) auf Mikrocontrollerbasis anhand des Lyrat V4.3 mit dem ESP32. Ziel der Arbeit ist es, die theoretischen und praktischen Grundlagen digitaler Biquad-Filter zu vermitteln und in einer anwendungsorientierten Lerndemonstration umzusetzen. Dabei werden verschiedene Filterstrukturen wie Direktform 1, Direktform 2 sowie die transponierte Direktform 2 in Arduino und MicroPython realisiert und miteinander verglichen. Der Fokus liegt auf der Audioverarbeitung, insbesondere der Verarbeitung von WAV-Dateien sowie die Echtzeit-Filterung über Mikrofoneingänge.

Ein zentraler Bestandteil des Gesamtprozesses ist der digitale Filterentwurf in Python. Mithilfe von Bibliotheken wie scipy.signal sowie dem Tool pyfda werden Biquads entworfen, analysiert und deren Koeffizienten zur Implementierung auf dem Mikrocontroller exportiert. Diese Vorgehensweise ermöglicht eine effiziente Verifikation der Filtereigenschaften im Vorfeld und bildet die Brücke zwischen Design und Hardwareumsetzung.

Durch die Kombination von theoretischen Grundlagen, grafischen Designwerkzeugen, kommentierten Codebeispielen und praxisnahen Anwendungen bietet diese Arbeit eine kompakte Anleitung für Studierende und Entwickler, um eigene digitale Filterlösungen auf Mikrocontrollern mit begrenzten Ressourcen zu realisieren und weiterzuentwickeln. Die gesamten Inhalte dieser Arbeit sind innerhalb eines Git Repositorys hinterlegt und dokumentiert.

5 Motivation

Die Motivation dieser Arbeit liegt darin, die erlernten Grundkenntnisse aus der Theorie in die Praxis umzusetzen. Im Rahmen des Studiums wurden die Grundlagen der digitalen Signalverarbeitung, insbesondere digitaler Filter, intensiv behandelt, jedoch meist in abstrakter und simulierter Form. Ziel dieser Thesis ist es daher, diese theoretischen Konzepte durch eine praxisnahe Anwendung auf echter Hardware greifbar zu machen und so ein tieferes Verständnis für deren Umsetzung und Verhalten im realen System zu gewinnen.

Im Mittelpunkt der Arbeit steht die Implementierung digitaler Biquad-Filter auf dem Lyrat-Audioboard mit dem ESP32. Dabei werden verschiedene Filterstrukturen wie Direktform 1, Direktform 2 und die transponierte Direktform 2 implementiert und im Hinblick auf ihre Eigenschaften verglichen. Neben der Entwicklung der Filterlogik in C++ (Arduino) und MicroPython werden auch praxisrelevante Anwendungsbeispiele realisiert, darunter die Echtzeitfilterung über den Mikrofoneingang sowie die Verarbeitung von WAV-Dateien von einer SD-Karte.

Ergänzend erfolgt der digitale Filterentwurf mithilfe von Python-Tools wie scipy.signal und pyfda, wodurch die benötigten Koeffizienten grafisch analysiert und direkt für die Implementierung aufbereitet werden können. Durch diese Verbindung aus Theorie, Software-Design und Hardwareumsetzung entsteht eine vollständige Lerndemonstration, die nicht nur den eigenen Lernfortschritt fördert, sondern auch als Hilfestellung für andere Studierende und Entwickler dienen kann, die sich mit digitaler Signalverarbeitung auf Mikrocontrollerbasis beschäftigen.

6 Einführung

Die digitale Signalverarbeitung ist ein zentraler Bestandteil moderner Audio- und Kommunikationstechnik. Insbesondere digitale Filter spielen eine entscheidende Rolle bei der Rauschunterdrückung, Signalglättung und Frequenzselektion. In ressourcenbeschränkten eingebetteten Systemen wie Mikrocontrollern müssen solche Filter effizient, stabil und echtzeitfähig implementiert werden. Eine weit verbreitete Struktur sind dabei Biquad-Filter, die sich durch geringe Rechenlast, gute Skalierbarkeit und hohe Flexibilität auszeichnen.

Ziel dieser Bachelorarbeit ist die systematische Entwicklung, Berechnung und Umsetzung digitaler Biquad-Filter auf dem Lyrat-Audioboard mit dem ESP32. Als praxisorientierte Lerndemonstration wird gezeigt, wie digitale Filter mit den verschiedenen Strukturen: Direktform 1, Direktform 2 und transponierte Direktform 2, auf Mikrocontrollern programmiert und eingesetzt werden können. Die Implementierung erfolgt in zwei Programmierumgebungen: Arduino und MicroPython. Im Vordergrund stehen dabei sowohl die Filterung von WAV-Dateien als auch die Echtzeitverarbeitung von Audiosignalen über den Mikrofoneingang.

Ein wichtiger Bestandteil des Workflows ist der digitale Filterentwurf in Python. Mit Hilfe von Bibliotheken wie SciPy, NumPy und dem Tool pyFDA werden die benötigten IIR-Koeffizienten entworfen, analysiert und für die spätere Implementierung auf dem Mikrocontroller vorbereitet. Durch die grafische Analyse lassen sich Frequenzgang, Stabilität und Quantisierungseinflüsse bereits im Vorfeld bewerten und optimieren. Der Entwurf in Python dient dabei als flexible und zugängliche Plattform zur Verifikation und Visualisierung der Filtereigenschaften, bevor die praktische Umsetzung auf dem Zielsystem erfolgt.

Die Arbeit richtet sich an Studierende und Entwickler, die sich mit digitaler Signalverarbeitung in eingebetteten Systemen beschäftigen. Sie kombiniert theoretische Grundlagen, praxisorientierte Entwurfswerkzeuge und kommentierte Codebeispiele, um einen umfassenden und anwendungsnahen Einstieg in die Implementierung digitaler Filter auf Mikrocontrollern zu bieten.

Diese Bachelorarbeit dokumentiert den Entwicklungs- und Implementierungsprozess, der im zugehörigen GitHub-Repository festgehalten wurde. Sowohl das Repository als auch Teile dieser Arbeit sind im Rahmen einer Zusammenarbeit mit einer parallel durchgeführten Bachelorarbeit entstanden, die eine vergleichbare Fragestellung behandelt. Da beide Arbeiten auf denselben theoretischen Grundlagen basieren, wurden diese gemeinsam erarbeitet. Auch der Vergleich der unterschiedlichen Implementierungsmethoden erfolgte in enger Abstimmung und wurde kollaborativ ausgearbeitet.

7 Filterimplementierung auf Mikrocontrollern

Die Zielhardware bei der Implementierung von digitalen IIR-Filtern auf Mikrocontroller ist das Lyrat V4.3 mit dem ESP32. Das Lyrat V4.3 ist ein Audio-Entwicklungsboard von Espressif Systems mit zwei Tensilica Xtensa LX6 Prozessorkernen welche bis zu 240 MHz Frequenz takten und einem 520 KB internem RAM. Dieses Board verfügt über einen ES8388 Audiocodec. Über diesen Codec werden Hardware-Ausstattung wie ein integriertes Stereo-Mikrofon für Audioaufnahme, AUX-IN und AUX-OUT Anschlüsse für externe Audioquellen und Audioausgabegeräte angesprochen. Über einen MicroSD-Kartenslot können WAV-Dateien als Audioquellen eingebunden werden. Diese Konfiguration ermöglicht sowohl die Verarbeitung von Audio-Streams in Echtzeit als auch die Filterung gespeicherter Audiodateien.

ESP Lyrat V4.3

7.1 Arduino Implementierung

Das Arduino-Framework basiert auf C/C++ und bietet durch spezialisierte Audio-Bibliotheken wie die arduino-audio-tools sowie die arduino-audio-driver von Phil Schatzmann eine Basis für die Echtzeitaudioverarbeitung. Bei der Implementierung werden die Programme mittels der Arduino IDE verfasst, kompiliert und auf den ESP32 geflasht.

7.2 Micropython Implementierung

MicroPython verwendet eine interpretierte Python-Syntax, die eine schnellere Entwicklung und vereinfachtes Debugging ermöglicht, jedoch aufgrund geringerer Ausführungsgeschwindigkeit primär für Prototyping geeignet ist und für keine hohen Verarbeitungsprozesse geeignet ist. Für die Implementierung in Micropython wird die ThonnyIDE mit dem Micropython Interpreter genutzt und der ESP32 wird mit einer Kompaktiblen Firmware geflasht.

7.3 Vorgehen bei der Implementierung

Für die Implementierung von digitalen Filtern auf Mikrocontrollern werde anhand der theoretischen Grundlagen die Strukturen durch ihre korrespondierenden Differenzengleichungen in Software umgesetzt. Diese Umsetzungen werden als Basis für weitere Verarbeitung von WAV-Datei genutzt. Im Folgenden werden die Strukturen in Arduino realisiert.

8 Implementierungserklärung der Biquad Filter in Arduino

Für die Implementierung der biquadratischen Filter in Arduino werden die Differenzengleichungen aus den Theoretischen Grundlagen entnommen und in Code umgesetzt. Die Filter sollen über das Einsetzten der b und a Koeffizienten implementiert werden.

8.1 Filter Basisklasse

class Filter
  {
  public:
    virtual ~Filter() {}
    virtual float filter(float) = 0;
  };

Diese abstrakte Basisklasse dient als Interface für alle Filterimplementierungsstrukturen. Der virtuelle Destruktor virtual ~Filter() {} stellt sicher, dass beim Löschen eines Objekts über einen Basisklassenzeiger der korrekte Destruktor der abgeleiteten Klasse aufgerufen wird. Die rein virtelle Methode virtual float filter(float) = 0; definiert die einheitliche Schnittstelle - jede abgeleitete Filterklasse muss eine filter() - Methode implementieren, die einen float-Wert entgegennimmt und einen gefilterten float-Wert zurückgibt. Diese Struktur ermöglicht die Verwendung der verschiedenen Filtertypen im Anwendiungsfall einer Kaskadierung.

8.2 Direktform 1

8.2.1 Private Member-Variablen

private:
  const float b_0; 
  const float b_1;
  const float b_2;
  const float a_1;
  const float a_2;

  float x_1 = 0;
  float y_1 = 0;
  float y_2 = 0;

Die Filterkoeffizienten b_0, b_1, b_2, a_1, a_2 sind als const deklariert, da sie nach der Initialisierung unveränderlich bleiben sollen. Dies entspricht der mathematischen Definition eines zeitinvarianten Systems. Die Verzögerungselemente x_1, y_1, y_2 speichern die vorherigen Ein- und Ausgangswerte. Der Wert a_0 wird nicht gespeichert, da durch die Normalisierung im Konstruktor alle Koeffizienten bereits durch a_0 geteilt wurden.

8.2.2 Konstruktor

BiquadFilterDF1(const float (&b)[3], const float (&a)[3], float gain)  
    : b_0(gain * b[0] / a[0]),
      b_1(gain * b[1] / a[0]),
      b_2(gain * b[2] / a[0]),
      a_1(a[1] / a[0]),
      a_2(a[2] / a[0]) 
{
}

Der Konstruktor verwendet Initialisierungslisten für optimale Performance. Die Koeffizienten werden direkt bei der Objekterstellung normalisiert, indem alle durch a[0] geteilt werden. Dies entspricht der Standardform der Differenzengleichung, wo der führende Koeffizient des Nenners auf 1 normiert wird. Der gain Parameter wird in die Zählerkoeffizienten eingerechnet, was mathematisch äquivalent zur Multiplikation der gesamten Übertragungsfunktion mit dem Verstärkungsfaktor ist. Die Array-Referenz-Syntax const float (&b)[3] stellt sicher, dass exakt drei Elemente übergeben werden müssen.

8.2.3 Filter Methode

float filter(float x_0)
{
  float x_2 = x_1;
  x_1 = x_0;
    
  float y_0 = b_0 * x_0 + b_1 * x_1 + b_2 * x_2 - a_1 * y_1 - a_2 * y_2;
    
  y_2 = y_1;
  y_1 = y_0;

  return y_0;
}

Diese Implementierung wird durch die Struktur der DF1 umgesetzt. Zuerst werden die Eingangsverzögerungen aktualiseirt: x_2 erhält den vorherigen Wert von x_1, dann wird x_1 auf den aktuellen Eingangswert x_0 gesetzt. Die Differenzengleichung wird direkt implementiert: y[n] = b_0 * x[n] + b_1 * x[n-1] + b_2 * x[n-2] - a_1 * y[n-1] - a_2 * y[n-2]. Im Anschluss werden die Ausgangsverzögerungen für die nächste Iteration aktualisiert. Diese Reihenfolge ist kritisch, da die Berechnung vor Aktualisierung der Ausgangsverzögerungen erfolgen muss.

8.3 Direktform 2

8.3.1 Private Member Variablen

private:
  const float b_0; 
  const float b_1;
  const float b_2;
  const float a_1;
  const float a_2;

  float w_0 = 0;
  float w_1 = 0;

Die DF2-Struktur benötigt nur zwei Verzögerungselemente w_0, w_1 anstatt der vier in DF1. Dies reduziert den Speicherbedarf um die 50%. Die w Variablen repräsentieren die internen Knotenpunkte der DF2-Struktur, wo sowohl die Rückkopplung als auch die Vorwärtskopplung zusammenlaufen.

8.3.2 Konstruktor

BiquadFilterDF2(const float (&b)[3], const float (&a)[3], float gain)  
    : b_0(gain * b[0] / a[0]),
      b_1(gain * b[1] / a[0]),
      b_2(gain * b[2] / a[0]),
      a_1(a[1] / a[0]),
      a_2(a[2] / a[0]) 
{
}

Der Konstruktor ist identisch zur DF1 Implementierung, da die Koeffizientennormalisierung unabhängig von der internen Filterstruktur ist. Die mathematische Übertragungsfunktion bleibt dieselbe, nur die interne Realisierung unterscheidet sich

8.3.3 Filter Methode

float filter(float x_0)
{
  float w_2 = w_1;
  w_1 = w_0;
  w_0 = x_0 - a_1 * w_1 - a_2 * w_2;

  float y_0 = b_0 * w_0 + b_1 * w_1 + b_2 * w_2;

  return y_0;
}

Die DF2 Implementierung teilt die Berechnung in zwei Phasen: Zuerst wird der interne Zustand w_0 berechnet, der das Eingangssignal minus der Rückkopplung darstellt. Dies entspricht der Implementierung des Nennerpols der Übertragungsfunktion. Dann wird der Ausgang durch die Vorwärtskopplung mit den b Koeffizienten berechnet, was dem Zählerpolynom entspricht. Die Verzögerungselemente werden vor der w_0 Berechnung aktualisiert, damit die korrekten vorherigen Werte verwendet werden.

8.4 Transponierte Direktfrom 2

8.4.1 Private Member Variablen

private:
  const float b_0; 
  const float b_1;
  const float b_2;
  const float a_1;
  const float a_2;

  float s_1 = 0;
  float s_2 = 0;

Die TDF2 Struktur verwendet Zustandsvariablen s_1, s_2, die als “shift register” fungieren. Diese Struktur ist die transponierte Version der DF2, was bedeutet, dass der Signalfluss umgekehrt wird: die Ein- und Ausgänge werden vertauscht, sowohl als auch die Richtung der Verzögerungselemente wird umgekehrt.

8.4.2 Konstruktor

BiquadFilterTDF2(const float (&b)[3], const float (&a)[3], float gain)  
    : b_0(gain * b[0] / a[0]),
      b_1(gain * b[1] / a[0]),
      b_2(gain * b[2] / a[0]),
      a_1(a[1] / a[0]),
      a_2(a[2] / a[0]) 
{
}

Auch hier ist der Konstruktor identisch zu den anderen Implementierungen, da die Koeffizientennormalisierung eine mathematische Anforderung ist, die unabhängig von der gewählten Realisierungsform gilt.

8.4.3 Filter Methode

float filter(float x_0)
{
  float y_0 = s_1 + b_0 * x_0;

  s_1 = s_2 + b_1 * x_0 - a_1 * y_0; 
  s_2 = b_2 * x_0 - a_2 * y_0;
    
  return y_0;
}

Bei der TDF2 Implementierung setzt sich der Ausgangswert aus der addition aus dem ersten Zustandsregister s_1 mit dem verstärkten Eingangswert. Die Zustandsregister werden dann für die nächste Iteration aktualisiert. s_1 wird zum nächsten Wert von s_2 addiert mit den gewichteten Ein- und Ausgangswerten. s_2 wird komplett neu berechnet. Diese Struktur hat den Vorteil, dass der Ausgangswert sehr früh im Berechnungszyklus verfügbar ist, was bei Pipeline Implementierungen sich als vorteilhaft erweisen kann.

8.5 Eingabe Koeffiziente

const float b_0 = f;
const float b_1 = f;
const float b_2 = f;
const float a_0 = f;
const float a_1 = f;
const float a_2 = f;

Bei den Eingabe-Koeffezienten wird der f Suffix an die float Literalen angehängt, sodass sicher gestellt wird das die Werte als singel-precision floating-point interpretiert werden, was bei Arduino-System von hoher Wichtigkeit ist.

8.6 Koeffizienten Arrays und Filter Instanziierung

const float b_coefficients[] = { b_0, b_1, b_2};
const float a_coefficients[] = { a_0, a_1, a_2};
const float gain = 1;

BiquadFilterTDF2 biquad(b_coefficients, a_coefficients, gain);

Die Koeffizienten werden in separaten Arrays gespeichert und an den Konstruktor übergeben. Dies ermöglicht eine saubere Trennung zwischen Filterdesign (Koeffizienten) und Implementierung (Filterklasse). Über den gain Paramter kann auf den zu Implementierenden Filter eine gewünschte Verstärkung angewandt werden. Bei einem Wert von 1 wird keine zusätzliche Verstärkung angewendet. Bei dieser Filter Instanziierung wird die TDF2 verwendet mir ihrem korosponierenden Klassennamen. Somit wird das Objekt biquad durch die Klasse BiquadFilterTDF2 instanziiert. Innerhalb des Objekts werden die Koeffizienten mit dem Verstärkungsfaktor an die jeweilige Filterklasse übergeben. Der Implementierte Filter steht bereit zur Verwendung.

8.7 Filter Anwendung

float filtered = biquad.filter(Input);

Die direkte Anwendung erfolgt durch den Aufruf der filter()-Methode auf dem Filterobjekt biquad. Der Eingangswert Input wird der Methode übergeben, durch die spezifische Filterimplementierung entsprechend der definierten Differenzengleichung verarbeitet und als transformierter Ausgangswert filtered zurückgegeben.

9 Filterung einer WAV Datei in Arduino

Zur Demonstration von digitalen Filtern auf Mikrocontrollern wird eine WAV-Datei mittels eines ESP32 gefiltert. Die Audio-Datei wird über eine SD-Karte eingelesen, gefiltert und als gefilterte Variante abgespeichert.

Zu beachten ist, dass nur 16-Bit-WAV-Dateien unterstützt werden. Die Datei kann jedoch Mono oder Stereo mit und einer beliebigen Samplerate sein. Die WAV-Datei, die gefiltert werden soll, muss zu original.wav umbenannt werden bevor diese auf die SD-Karte übertragen wird.

9.1 Vorbereitung der WAV-Filterung

#include "SD_MMC.h" // SD-Karten-Support für ESP32 mit SD_MMC-Anschluss

Durch die Einbindung vom SD_MMC.h wird eine erleichterte Nutzung von SD-Karten mit einem ESP32 geboten, als auch die Möglichkeit für 1-Wire-Modus sowie 4-Wire-Modus.

// --- WAV Hilfsfunktionen ---
uint32_t readLEUint32(uint8_t* buf) {
  return (uint32_t)buf[0] | ((uint32_t)buf[1] << 8) 
  | ((uint32_t)buf[2] << 16) | ((uint32_t)buf[3] << 24);
}
uint16_t readLEUint16(uint8_t* buf) {
  return (uint16_t)buf[0] | ((uint16_t)buf[1] << 8);
}

Diese Hilfsfunktionen konvertieren Byte-Arrays aus WAV-Dateien in Ganzzahlen im Little-Edian-Format um. readLEUint32() kombiniert 4 Bytes zu einem 32-Bit-wert, readLEUint16() kombiniert 2 Bytes zu einem 16-Bit-Wert, wobei das niedrigste Byte zuerst kommt.

// WAV-Header für die Ausgabedatei schreiben
void writeWavHeader(File &file, uint32_t dataSize, uint16_t channels, 
uint32_t sampleRate, uint16_t bitsPerSample) {
  const char* riff = "RIFF";
  const char* wave = "WAVE";
  const char* fmt  = "fmt ";
  const char* data = "data";

  uint32_t chunkSize = 36 + dataSize;
  uint16_t blockAlign = channels * bitsPerSample / 8;
  uint32_t byteRate = sampleRate * blockAlign;
  uint32_t subchunk1Size = 16;
  uint16_t audioFormat = 1; // PCM

  file.seek(0);
  file.write((const uint8_t*)riff, 4);
  file.write((uint8_t*)&chunkSize, 4);
  file.write((const uint8_t*)wave, 4);
  file.write((const uint8_t*)fmt, 4);
  file.write((uint8_t*)&subchunk1Size, 4);
  file.write((uint8_t*)&audioFormat, 2);
  file.write((uint8_t*)&channels, 2);
  file.write((uint8_t*)&sampleRate, 4);
  file.write((uint8_t*)&byteRate, 4);
  file.write((uint8_t*)&blockAlign, 2);
  file.write((uint8_t*)&bitsPerSample, 2);
  file.write((const uint8_t*)data, 4);
  file.write((uint8_t*)&dataSize, 4);
}

Die writeWavHeader-Funktion schreibt einen WAV-Header in die Ausgabedatei. Die Funktion erstellt die erforderlichen Chunks (RIFF, WAVE, fmt, data) mit den übergebenen Audio-Parametern und berechnet automatisch die abgeleiteten Werte wie Byte-Rate und Block-Alignment. Der Header wird im Little-Endian-Format geschrieben.

// --- Variablen für die Ein- und Ausgangsdatei --
File wavFile;       // Originale Eingangsdatei
File filteredFile;  // Gefiltere Ausgangsdatei

Hilfsvariablen für die originale Eingangsdatei als auch die gefilterte Ausgangsdatei.

Der Gesamtprozess bestehend aus einlesen, filtern und neuen WAV-Datei erstellen wird innerhalb der Setup()-Funktion durchgeführt.

void setup() {
  Serial.begin(115200);

Zunächst wird die serielle Kommunikation mit 115200 Baud initialisiert, um Informationen des Mikrocontroller in der Konsole auslesen zu können.

// SD-Karte im 4-Wire Modus initialisieren
if (!SD_MMC.begin("/sdcard", false)) {  //false = 4-Wire, true - 1-Wire
  Serial.println("Fehler beim Initialisieren der SD-Karte.");
  return;
}
Serial.println("SD-Karte gefunden.");

Die SD-Karte wird im 4-Wire-Modus initialisiert, welcher eine höhere Datenübertragungsrate ermöglicht als der 1-Wire-Modus. Durch den Parameter false wird der 4-Wire-Modus aktiviert, während true den 1-Wire-Modus aktiviert. Wird keine SD-Karte gefunden oder besteht ein Problem bei der Initialisierung, wird eine Fehlermeldung ausgegeben und das Programm beendet.

// Eingangs WAV Datei öffnen
wavFile = SD_MMC.open("/original.wav", FILE_READ);
if (!wavFile) {
  Serial.println("Fehler beim Öffnen der WAV-Datei.");
  return;
}

// WAV Header auslesen
if (!readWavHeader()) {
  wavFile.close();
  return;
}

Die originale WAV-Datei wird im Lesemodus geöffnet. Für den Fall, dass das Öffnen fehlschlägt, wird dementsprechende Fehlermeldung ausgegeben und das Programm beendet. Bei erfolgreichen Öffnen wird die Funktion readWavHeader aufgerufen und der Header der Eingangsdatei analysiert. Falls diese Funktion false zurückgibt, wird die Datei geschlossen und das Programm beendet.

bool readWavHeader() {
  uint8_t riffHeader[12];
  if (wavFile.read(riffHeader, 12) != 12) {
    Serial.println("Fehler beim Lesen des RIFF-Headers.");
    return false;
  }
  //Prüfen auf "RIFF" und "WAVE"
  if (memcmp(riffHeader, "RIFF", 4) != 0 || memcmp(&riffHeader[8],
   "WAVE", 4) != 0) {
    Serial.println("Keine gültige WAV-Datei.");
    return false;
  }

Die Header-Analyse-Funkion beginnt mit der Validierung der WAV-Datei Signatur. Dazu werden die ersten 12 Bytes der Datei gelesen, die den RIFF-Header bilden. Anschließend wird überprüft, ob die Bytes 0-3 die Zeichenkette “RIFF” und die Bytes 8-11 die Zeichenkette “WAVE” enthalten. Diese Signaturen sind für alle gültigen WAV-Dateien notwendig und identifizieren das genaue Dateiformat.

// Variablen für WAV-Informationen
uint16_t audioFormat = 0, numChannels = 0, bitsPerSample = 0;
uint32_t sampleRate = 0, dataSize = 0;
bool fmtFound = false, dataFound = false;

Für die Chunk-Analyse werden die folgenden Variablen initialisiert, welche die Audio-Parameter speichern. Die 16-Bit Variablen audioFormat, numChannels und bitsPerSample enthalten die grundlegenden Format-Informationen, während sampleRate und dataSize als 32-Bit-Werte die Abtastrate und Datengröße speichern. Die booleschen Flags fmtFound und dataFound verfolgen, die notwendigen Chunks bereits gefunden wurden.

// Suche nach "fmt " und "data" Chunks
while (wavFile.position() < wavFile.size()) {
  uint8_t chunkHeader[8];
  if (wavFile.read(chunkHeader, 8) != 8) {
    Serial.println("Fehler beim Lesen eines Chunk-Headers.");
    break;
  }
  uint32_t chunkSize = readLEUint32(&chunkHeader[4]);

Der Chunk-Parser durchläuft systematisch die WAV-Datei, um relevante Datenabschnitte zu finden. Die WAV-Datei ist in Chunks unterteilt, die jeweils mit einem 8-Byte-Header beginnt: 4 Bytes für die Chunk-ID und 4 Bytes für die Größe im Little-Endian-Format. Die Schleife läuft bis zum Dateiende oder bis ein Lesefehler auftritt.

//Format-Chunk gefunden
if (memcmp(chunkHeader, "fmt ", 4) == 0) {
  uint8_t fmtChunk[chunkSize];
  if (wavFile.read(fmtChunk, chunkSize) != chunkSize) {
    Serial.println("Fehler beim Lesen des fmt-Chunks.");
    break;
  }
  audioFormat = readLEUint16(&fmtChunk[0]);
  numChannels = readLEUint16(&fmtChunk[2]);
  sampleRate = readLEUint32(&fmtChunk[4]);
  bitsPerSample = readLEUint16(&fmtChunk[14]);
  fmtFound = true;

  // Parameter der Eingangs-WAV
  Serial.printf("AudioFormat: %d\n", audioFormat);
  Serial.printf("Kanäle: %d\n", numChannels);
  Serial.printf("SampleRate: %d\n", sampleRate);
  Serial.printf("Bits pro Sample: %d\n", bitsPerSample);

  if (chunkSize % 2 == 1) wavFile.seek(wavFile.position() + 1);
}

Wenn der Chunk-Header “fmt” gefunden wird, werden die Chunk-Daten in einen Puffer geladen und die wichtigsten Audio-Parameter extrahiert: Audi-Format(PCM), Kanalzahl(Mono oder Stereo), Samplerate und die Bits pro Sample aus festen Byte-Positionen. Die Parameter werden zur Kontrolle ausgegeben und bei ungerader Chunk-Größe wird ein Padding-Byte übersprungen.

// Daten-Chunk gefunden
else if (memcmp(chunkHeader, "data", 4) == 0) {
  dataSize = chunkSize;
  dataFound = true;
  break;
}

Der Data-Chunk enthält die eigentlichen Audio-Daten mit den Samples. Sobald dieser gefunden wird, wird seine Größe gespeichert und die Suche endet. Der Dateizeiger steht dann am Beginn der Audio-Samples für die weitere Verarbeitung.

  // Irrelavante Chucks überspringen
  else {
    wavFile.seek(wavFile.position() + chunkSize);
    if (chunkSize % 2 == 1) wavFile.seek(wavFile.position() + 1);
  }
}

Irrelevante Chunks, wie LIST oder INFO, werden übersprungen, indem der Dateizeiger um die Chunk-Größe voranbewegt wird. Bei ungerader Chunk-Größe wird ein zusätzliches Padding-Byte übersprungen.

// Überprüfen ob alle nötigen Informationen gefunden wurden
if (!fmtFound || !dataFound) {
  Serial.println("WAV-Header unvollständig oder Datenchunk nicht gefunden.");
  return false;
}

if (audioFormat != 1) {
  Serial.println("Nur PCM WAV-Dateien werden unterstützt.");
  return false;
}

if (bitsPerSample != 16) {
  Serial.println("Nur 16-Bit PCM wird unterstützt.");
  return false;
}

if (numChannels != 1 && numChannels != 2) {
  Serial.println("Nur Mono oder Stereo wird unterstützt.");
  return false;
}

Es wird überprüft, ob Format- und Data-Chunk gefunden wurden und ob die Datei das kompatible Format besitzt. Entspricht die Datei nicht dem vorgesetzten Format wird eine Fehlermeldung ausgeben und das Programm beendet.

// Ausgabedatei erstellen und Header schreiben
filteredFile = SD_MMC.open("/gefiltert.wav", FILE_WRITE);
if (!filteredFile) {
  Serial.println("Fehler beim Öffnen der Ausgabedatei.");
  return false;
}

writeWavHeader(filteredFile, dataSize, numChannels, sampleRate, bitsPerSample);

Serial.printf("Gesamtanzahl Frames (Samples pro Kanal): %d\n", 
              dataSize / (numChannels * bitsPerSample / 8));
Serial.println("Starte Filterung...");

// Filterprozess starten
filterAudio(numChannels, dataSize, bitsPerSample);

Serial.println("Filterung abgeschlossen.");

wavFile.close();
filteredFile.close();

return true;

Die Ausgabedatei “gefiltert.wav” wird im Schreibmodus erstellt und erhält einen neuen WAV-Header mit den identischen Parametern der Eingangsdatei. Würde man keinen neuen WAV-Header erstellen, sondern den bestehenden verwenden, würde die resultierende Datei fehlerhaft enden. Es werden die Anzahl der Frames berechnet und ausgeben, und im Anschluss wird die Sample-für-Sample Filterung über die filterAudio()-Funktion gestartet. Nach der Filterung werden beide Dateien geschlossen und endet damit das Programm.

9.2 Filterprozess der WAV-Datei

// --- Filterprozess auf Samples der WAV anwenden ---
void filterAudio(uint16_t numChannels, uint32_t dataSize, uint16_t bitsPerSample) {
  uint16_t blockAlign = numChannels * bitsPerSample / 8;
  const int bufferFrames = 512;
  int16_t buffer[bufferFrames * numChannels]; // Zwsichenspeicher für Samples

  uint32_t totalFrames = dataSize / blockAlign;
  uint32_t framesLeft = totalFrames;

  while (framesLeft > 0) {
    int framesToRead = (framesLeft > bufferFrames) ? bufferFrames : framesLeft;
    int bytesToRead = framesToRead * blockAlign;

    // Rohdaten lesen
    int bytesRead = wavFile.read((uint8_t*)buffer, bytesToRead);
    if (bytesRead != bytesToRead) {
      Serial.println("Fehler beim Lesen der Samples.");
      break;
    }

    int samplesInBuffer = bytesRead / 2; // 2 Bytes = 16 Bit pro Sample


    // Samples einzeln filtern
    for (int i = 0; i < samplesInBuffer; i += numChannels) {
      if (numChannels == 1) {
        float filteredSample = filterL.filter((float)buffer[i]);
        buffer[i] = constrain((int)filteredSample, -32768, 32767);
      }
      else {
        float filteredL = filterL.filter((float)buffer[i]);
        float filteredR = filterR.filter((float)buffer[i + 1]);
        buffer[i] = constrain((int)filteredL, -32768, 32767);
        buffer[i + 1] = constrain((int)filteredR, -32768, 32767);
      }
    }
    // Gefilterte Daten in neue Datei schreiben
    filteredFile.write((uint8_t*)buffer, bytesRead);
    framesLeft -= framesToRead;

Die filterAudio-Funktion führt die Sample-für-Sample-Verabreitung der Audio-Daten durch.

Blockweise Verarbeitung: Die Audio-Daten werden in 512-Frame-Blöcken eingelesen, anstatt die gesamte Datei in den Speicher zu laden. Die ermöglicht auch die Verarbeitung großer Dateien mit begrenztem Arbeitsspeicher.

Filteranwendung: Jedes der Sample wird durch die digitalen Filter gesendet. Bei Mono wird jeweils jedes Sample durch eine einzige Filterinstanz (filterL) verarbeitet. Bei Stereo liegen die 16-Bit-Samples im Interleaved-Format vor, bei welchem sich der linken und rechten Kanalsamples abwechseln(LRLRLR…). Die Schleife springt um numChannels Positionen (i +=numChannels), wodurch buffer[i] stets den linken und buffer[i] den rechten Kanal adressiert. Beide Kanäle werden durch separate Filterinstanzen (filterL für links, filterR für rechts) unabhängig voneinander gefiltert, was die Stereo-Trennung gewährleistet.

Wertebreichsschutz: Da digitale Filter die Amplitude verstärken können, werden die gefilterten Werte mit constrain() auf den gültigen 16-Bit-Bereich begrenzt. Dies verhindert Übersteuerung und damit verbundene Verzerrungen.

Kontinuierliche Ausgabe: Die verarbeiteten Samples werden sofort in die Ausgabedatei geschrieben, wodurch ein kontinuierlicher Datenfluss ohne große Zwischenspeicherung gewährleistet wird.

9.3 Filterkaskadierung

Die Kaskadierung wird durchgeführt, indem die Filterung durch mehrere Stufen durchgeführt wird. Diese Stufen können durch Biquad-Filter oder Segmente einer SOS-Matrix definiert werden.

#define NUM_STAGES 2 // Anzahl der Filterstufen

// Erste Sektion
const float gain_s1 = 1.0;
const float b_coefficients_s1[] = { b_0_s1, b_1_s1, b_2_s1};
const float a_coefficients_s1[] = { a_0_s1, a_1_s1, a_2_s1};
// Zweite Sektion
const float gain_s2 = 1.0;
const float b_coefficients_s2[] = { b_0_s2, b_1_s2, b_2_s2};
const float a_coefficients_s2[] = { a_0_s2, a_1_s2, a_2_s2};

BiquadFilterTDF2 filterL[NUM_STAGES] = {
  BiquadFilterTDF2(b_coefficients_s1, a_coefficients_s1, gain_s1),
  BiquadFilterTDF2(b_coefficients_s2, a_coefficients_s2, gain_s2),
};

BiquadFilterTDF2 filterR[NUM_STAGES] = {
  BiquadFilterTDF2(b_coefficients_s1, a_coefficients_s1, gain_s1),
  BiquadFilterTDF2(b_coefficients_s2, a_coefficients_s2, gain_s2),
};

Anhand des Parameters NUM_STAGES kann die Anzahl der Biquad-Sektionen definiert werden. Jede Sektion hat ihre eigenen b- und a-Koeffizienten sowie einen gain-Parameter mit den entsprechenden Bezeichnungen. Die Filterinstanzierung erfolgt durch Arrays von Biquad-Filtern, wobei jedes Array-Elemement eine separate Filtersstufe mit eigenen Koeffizienten repräsentiert.

Werden identische Filterparameter in mehrere Filterstufen implementiert, wird die Filtercharakteristik der vorherigen Stufe verstärkt. Alternativ können Filter höherer Ordnung implementiert werden, indem die SOS-Matrix etappenweise auf die einzelnen Filterstufen aufgeteilt wird.

// Samples einzeln filtern - KASKADIERT
for (int i = 0; i < samplesInBuffer; i += numChannels) {
  if (numChannels == 1) {
    float sample = (float)buffer[i];
    for (int s = 0; s < NUM_STAGES; s++) {
      sample = filterL[s].filter(sample);
    }
    buffer[i] = constrain((int)sample, -32768, 32767);
  }
  else {
    float left = (float)buffer[i];
    float right = (float)buffer[i + 1];
    for (int s = 0; s < NUM_STAGES; s++) {
      left = filterL[s].filter(left);
      right = filterR[s].filter(right);
    }
  buffer[i] = constrain((int)left, -32768, 32767);
  buffer[i + 1] = constrain((int)right, -32768, 32767);
}

Bei der kaskadierten Filterung werden die Filterstufen in Serie Implementiert, bei welcher die Samples durch jede Stufe sequenziell verarbeitet werden. Das Ausgangssignal einer Stufe wird zum Eingangssignal der nächsten Stufe, wodurch eine erhöhte Filterordnung oder verstärkte Filterwirkung ermöglicht. Bei Mono druchläuft jedes Sample alle NUM_STAGES Filterstufen des filterL-Arrays, bei Stereo werden beide Kanäle parallel durch ihre jeweiligen Filterkaskaden(filterL und filterR) verarbeitet. Nach der kompletten Kaskadierung werden die gefilterten Daten auf den 16-Bit-Bereich begrenzt und zurückgeschrieben.

10 Implementierungserklärung der Biquad Filter in Micropython

Für die Implementierung der biquadratischen Filter in Micropython werden die Differenzengleichungen aus den theoretischen Grundlagen entnommen und in Code umgesetzt. Die Filter werden über das Einsetzen der b und a Koeffizienten implementiert. Die DF1, DF2 und TDF2 werden als Klassen umgesetzt.

10.1 Micropython-Native Optimierung

import micropython

@micropthon.native
def filter(self,x0):

Der @micropython.native Decorator kompiliert die filter() Methoden zu nativem Maschinencode, was eine erhebliche Leistungssteigerung bei rechenintensiven Operationen ermöglicht.

10.2 __slots__Optimierung

__slots__=('b0', 'b1', 'b2', 'a2', 'gain')`

Alle Filterklassen verwenden __slots__, um den Speicherverbrauch zu reduzieren und die Attributzugriffe zu beschleunigen. Dies verhindert, dass Python ein dynamisches Dictionary für jede Instanz erstellt, wodurch sowohl Speicher als auch Zugriffszeit gespart werden.

10.3 Direktform 1

10.3.1 Instanzvariablen

class BiquadFilterDF1:
    __slots__ = ('b0', 'b1', 'b2', 'a1', 'a2', 'gain', 'x1', 'x2', 'y1', 'y2')

Die Filterkoeffizienten b0, b1, b2, a1, a2 werden nach der Initialisierung im Konstruktor nicht mehr verändert, was der mathematischen Definition eines zeitinvarianten Systems entspricht. Die Verzögerungselemente x1, x2 speichern die vorherigen Eingangswerte, während y1, y2 die vorherigen Ausgangswerte speichern. Der Wert a0 wird nicht gespeichert, da durch die Normalisierung im Konstruktor alle Koeffizienten bereits durch a[0] geteilt wurden.

10.3.2 Konstruktor

    def __init__(self, b, a, gain=1):
        self.gain = gain
        self.b0 = self.gain * (b[0] / a[0])
        self.b1 = self.gain * (b[1] / a[0])
        self.b2 = self.gain * (b[2] / a[0])
        self.a1 = a[1] / a[0]
        self.a2 = a[2] / a[0]
        self.x1 = 0.0
        self.x2 = 0.0
        self.y1 = 0.0
        self.y2 = 0.0

Der Konstruktor normalisiert alle Koeffizienten druch die Division mit a[0], wodurch die Standardform der Differenzengleichung erreicht wird. Dies entspricht der Standardform, wo der führende Koeffizient des Nenners auf 1 normiert wird. Der gain Parameter wird in die Zählerkoeffizienten eingerechnet, was mathematisch äquivalent zur Multiplikation der gesamten Übertragungsfunktion mit dem Verstärkungsfaktor ist. Die Verzögerungselemente werden auf 0.0 initialisiert, was einem System ohne vorherigen Werte entspricht.

10.3.3 Filter Methode

    @micropython.native
    def filter(self, x0):
        y0 = (self.b0 * x0 + self.b1 * self.x1 + self.b2 * self.x2 
            - self.a1 * self.y1 - self.a2 * self.y2)
        self.x2 = self.x1
        self.x1 = x0
        self.y2 = self.y1
        self.y1 = y0
        return y0

Für die Implementierung der DF1 wird die Differenzengleichung dieser Struktur direkt implementiert: y[n] = b0 * x[n] + b1 * x[n-1] + b2 * [x-2] - a1 * y[n-1] - a2 * y[n-2]. Anschließend werden die Verzögerungselemente für die nächste Iteration aktualisiert. Die Eingangsverzögerung werden durch self.x2 = self.x1 und self.x1 = x0 verschoben, während die Ausgangsverzögerung durch self.y2=self.y1 und self.y1 = y0 aktualisiert werden. Diese Reihenfolge ist kritisch, da die Berechnung vor der Aktualisierung der Ausgangswerte erfolgen muss.

10.4 Direktform 2

10.4.1 Instanzvariablen

class BiquadFilterDF2:
    __slots__ = ('b0', 'b1', 'b2', 'a1', 'a2', 'gain', 'w0', 'w1', 'w2')

Die DF2-Struktur benötigt drei Verzögerungselemente w0, w1, w2 statt der vier in der DF1. Dies reduziert den Speicherbedarf gegenüber der DF1. Die w Variablen repräsentieren die internen Knotenpunkte der DF2-Struktur, wo sowohl die Rückkopplung als auch die Vorwärtskopplung zusammenlaufen.

10.4.2 Konstruktor

    def __init__(self, b, a, gain=1):
        slef.gain = gain
        self.b0 = self.gain * (b[0] / a[0])
        self.b1 = self.gain * (b[1] / a[0])
        self.b2 = self.gain * (b[2] / a[0])
        self.a1 = a[1] / a[0]
        self.a2 = a[2] / a[0]
        self.w0 = 0.0
        self.w1 = 0.0
        self.w2 = 0.0

Der Konstruktor ist geradezu identisch zur DF1 Implementierung, da die Koeffizientennormalisierung unabhängig von der internen Filterstruktur ist. Der Unterschied liegt in der Vordefinition der Verzögerungselemente self.w0, self.w1, self.w2, welchen der Wert von 0.0 zugewiesen wird.

10.4.3 Filter Methode

    @micropython.native
    def filter(self, x0):
        y0 = self.b0 * self.w0 + self.b1 * self.w1 + self.b2 * self.w2
        self.w0 = x0 - self.a1 * self.w1 - self.a2 * self.w2
        self.w2 = self.w1
        self.w1 = self.w0
        return y0

Die DF2 Implementierung teilt die Berechnung in zwei Phasen: Zuerst wird der Ausgang aus den aktuellen Zustandsvariablen und den Zählerkoeffizienten berechnet. Dies entspricht der Implementierung des Zählerpolynoms der Übertrangungsfunktion. Dann wird der neue Zustand self.w0 berechnet, der das Eingangssignal minus der Rückkopplung darstellt. Die Verzögerungselemente werden durch self.w2 = self.w1 und self.w1 = self.w0 für die nächste Iteration verschoben.

10.5 Transponierte Direktform 2

10.5.1 Instanzvariablen

class BiquadFilterTDF2:
    __slots__ = ('b0', 'b1', 'b2', 'a1', 'a2', 'gain', 's1', 's2')

Die TDF2-Struktur verwendet Zustandsvariablen s1, s2, die als “shift register” fungieren. Diese Struktur ist die transponierte Version der DF2, was bedeutet, dass der Signalfluss umgekehrt wird: die Ein- und Ausgänge werden vertauscht, sowie die Richtung der Verzögerungselemente wird umgekehrt.

10.5.2 Konstruktor

   def __init__(self, b, a, gain=1):
        slef.gain = gain
        self.b0 = self.gain * (b[0] / a[0])
        self.b1 = self.gain * (b[1] / a[0])
        self.b2 = self.gain * (b[2] / a[0])
        self.a1 = a[1] / a[0]
        self.a2 = a[2] / a[0]
        self.s1 = 0.0
        self.s2 = 0.0

Auch hier ist der Konstruktor identisch zu den anderen Implementierungen, da die Koeffizientennormalisierung eine mathematische Anforderung ist, die unabhängig von der gewählten Realisierungsform gilt. In diesem Konstruktor werden die Variablen self.s1, self.s2 auf 0.0 gesetzt.

10.5.3 Filter Methode

    @micropython.native
    def filter(self, x0):
        y0 = self.b0 * x0 + self.s1
        self.s1 = self.s2 + self.b1 * x0 - self.a1 * y0
        self.s2 = self.b2 * x0 - self.a2 * y0
        return y0

Bei der TDF2 Implementierung setzt sich der Ausgangswert aus der Addition aus dem ersten Zustandsregister self.s1 mit dem verstärkten Eingangswert zusammen. Die Zustandsregister werden dann für die nächste Iteration aktualisiert. self.s1wird zum nächsten Wert von self.s2 addiert mit den gewichteten Ein- und Ausgangswerten. self.s2 wird komplett neu berechnet. Diese Struktur hat den Vorteil, dass der Ausgangswert sehr früh im Berechnungszyklus verfügbar ist, was bei Pipeline Implementierung vorteilhaft ist.

10.6 Filter Anwendung

from biquad import BiquadFilterTDF2

Für die Verwendung der Biquad-Filter wird aus der biquad.py die gewünschte Filterimplementierung importiert.

b = [1.0, 0.5, 0.25]
a = [1.0, -0.3, 0.1]
gain = 1.0

biquad = BiquadFilterTDF2(b, a, gain)

Die Koeffizienten werden in separaten Listen gespeichert und an den Konstruktor übergeben. Über den gain Parameter kann auf den zu implementierenden Filter eine gewünschte Verstärkung angewandt werden. Bei dieser Filter Instanziierung wird die TDF2 verwendet mit ihren entsprechenden Klassennamen. Somit wird das Objekt biquad durch die Klasse BiquadFilterTDF2 instanziiert. Innerhalb des Objekts werden die Koeffizienten mit dem Verstärkungsfaktor an die jeweilige Filterklasse übergeben und der Filter steht bereit zur Verwendung.

filtered = biquad.filter(input)

Die direkte Anwendung erfolgt durch den Aufruf der filter()-Methode auf dem Filterobjekt biquad. Der Eingangswert input wird der Methode übergeben, durch die spezifische Filterimplementierung entsprechend der definierten Differenzengleichung verarbeitet und als transformierter Ausgangswert filtered zurückgegeben.

11 Filterung einer WAV Datei in Micropython

Zur Demonstration von digitalen Filtern in Micropython wird eine WAV-Datei mittels eines ESP32 gefiltert. Die Audio-Datei wird über eine SD-Karte eingelesen, gefiltert und als gefilterte Variante abgespeichert.

Zu beachten ist, dass nur 16-Bit-WAV-Dateien unterstützt werden. Die Datei kann jedoch Mono oder Stereo mit und einer beliebigen Samplerate sein. Die WAV-Datei, die gefiltert werden soll, muss zu input.wav umbenannt werden bevor diese auf die SD-Karte übertragen wird.

11.1 Vorbereitung des Programms

import micropython, struct, os,
from machine import SDCard, freq
from biquad import BiquadFilterTDF2

Für die Filterung einer WAV-Datei werden die folgenden Module eingebunden: micropython ermöglicht die Optimierung durch native Deklaration, struct dient der binären Datenverarbeitung, os wird für Dateizugriffe genutzt und SDCard stellt die Schnittstelle zur SD-Karte bereit, während mit freq die CPU-Frequenz gesetzt werden kann. Aus der erstellten biquad.py wird die BiquadFilterTDF2 importiert.

freq(240000000)

Die CPU-Frequenz wird auf 240 MHz gesetzt, um maximale Rechenleistung des ESP32 für die Filterverarbeitung zu gewährleisten.

os.mount(SDCard(slot=1, width=4), "/sd")

Die SD-Karte wird über das SPI-Interface mit 4-Bit Breite gemountet, um höhere Datenübertragungsraten zu ermöglichen.

11.2 Konfiguration der Audioverarbeitung

Audio-Parameter

INPUT = "/sd/input.wav"
OUTPUT = "/sd/output_filtered.wav"
HEADER_SIZE = 44
CHANNELS = 2
BITS = 16
BYTES_PER_SAMPLE = BITS // 8
BYTES_PER_FRAME = CHANNELS * BYTES_PER_SAMPLE
BLOCK_FRAMES = 13200  # Je nach RAM anpassen
BLOCK_SIZE = BLOCK_FRAMES * BYTES_PER_FRAME

Die Konstanten definieren die Audioparameter für Stereo-WAV-Dateien mit 16-Bit Auflösung. Die BLOCK_FRAMES beeinflussen den Speicherverbrauch vom RAM und die Verarbeitungseffizienz. Der HEADS_SIZE von 44 Bytes entspricht der Standardgröße eines WAV-Headers.

Filter-Instanziierung

b = [0.07033, -0.1380, 0.07033]
a = [1.00000, -0.1380, -0.8593]
gain = 1.0
filtL = BiquadFilterTDF2(b, a, gain)
filtR = BiquadFilterTDF2(b, a, gain)

Für die Filterung vom Stereo-Format werden zwei Filterinstanzen, filtL für den linken Kanal und filtR für den rechten Kanal, erstellt.

11.3 WAV-Header Erstellung

def write_header(f, frames):
    rate = 44100
    byte_rate = rate * CHANNELS * BYTES_PER_SAMPLE
    align = CHANNELS * BYTES_PER_SAMPLE
    size = frames * align
    f.write(struct.pack("<4sI4s4sIHHIIHH4sI",
        b'RIFF', 36 + size, b'WAVE',
        b'fmt ', 16, 1, CHANNELS, rate,
        byte_rate, align, BITS,
        b'data', size
    ))

Die write_header() Funktion generiert einen standardkonformen WAV-Header im Little-Endian Format. Der Header enthält alle notwendigen Informationen: Dateigröße, Audioformat(PCM), Kanalanzahl, Abtastrate und Bit-Tiefe. Das struct.pack() mit "<4sI4s4sIHHIIHH4sI" Format sorgt für die korrekte Byte-Reihenfolge auf verschiedenen Plattformen.

11.4 Blockverarbeitung

@micropython.native
def process_block_native(read_mv, write_mv, sample_count, filtL, filtR):
    for i in range(0, sample_count, 2):
        # Samples einlesen (Little Endian)
        sL = read_mv[i*2] | (read_mv[i*2 + 1] << 8)
        sR = read_mv[i*2 + 2] | (read_mv[i*2 + 3] << 8)
        if sL >= 32768:
            sL -= 65536
        if sR >= 32768:
            sR -= 65536

Zur Optimierung wird mit dem @micropython.native Decorator die Verarbeitungsschleife zu nativem Maschinencode kompiliert. Die Verwendung von memoryview Objekten vermeidet Speicherkopien und reduziert die Garbage Collection. Die Schleife iteriert in 2er-Schritten durch sample_count, die jeweils ein Stereo-Sample verarbeitet wird.

Sample-Konvertierung

Die 16-Bit-Samples werden aus dem Byte-Array im Little-Endian Format rekonstruiert. Die bitweise OR-Operation kombiniert die Low- und High-Bytes: das erste Byte wird als niederwertige Bits verwendet, das zweite Byte wird um 8 nach links verschoben für die höherwertigen Bits. Die anschließende Überprüfung konvertiert unsigned 16-Bit Werte in signed Werte durch die Subtraktion von 65536 für Werte über 32767.

11.5 Filterung und Clamping

    l = int(filtL.filter(sL))
    r = int(filtR.filter(sR))

    if l > 32767: l = 32767
    elif l < -32768: l = -32768
    if r > 32767: r = 32767
    elif r < -32768: r = -32768

    struct.pack_into("<hh", write_mv, i*2, l, r)

Bei der Filterung werden die Samples auf ganze Zahlen gerundet und auf den gültigen 16-Bit Bereich begrenzt. Das Clamping verhindert Überläufe und damit verbundene Verzerrung im Ausgangssignal. Die Begrenzung ist notwendig, da die Filteroperation Werte außerhalb des ursprünglichen Bereichs erzeugen kann. Abschließend werden die verarbeiteten Samples mit struct.pack_into() direkt in den Ausgabepuffer geschrieben. Das Format "<hh" definiert zwei signed 16-Bit Integers im Little-Endian Format.

11.6 Hauptverarbeitung

    read_buf = bytearray(BLOCK_SIZE)
    write_buf = bytearray(BLOCK_SIZE)
    read_mv = memoryview(read_buf)
    write_mv = memoryview(write_buf)

Separate Read- und Write-Puffer ermöglichen effiziente Ein- und Ausgabeoperationen ohne Interferenz. Die memoryview Objekte bieten direkten Zugriff auf die Pufferdaten ohne Kopieroperationen, wodurch die Performance verbessert wird.

with open(INPUT, "rb") as fin, open(OUTPUT, "wb") as fout:
    fin.seek(HEADER_SIZE)
    write_header(fout, 0)

    while True:
        read_bytes = fin.readinto(read_buf)
        if read_bytes == 0:
            break

        sample_count = read_bytes // 2  # 2 Bytes pro Sample (16 Bit)

        # Verarbeitung mit native-Code
        process_block_native(read_mv, write_mv, sample_count, filtL, filtR)

        fout.write(write_mv[:read_bytes])
        frames += read_bytes // BYTES_PER_FRAME
        last = progress(frames, total, last)

Über den with Context Manager wird die Eingangsdatei geöffnet. Zunächst wird der WAV-Header der Eingangsdatei mit fin.seek(HEADER_SIZE) übersprungen und ein temporärer Header mit 0 Frames in die Ausgabedatei geschrieben. Die Verarbeitungsschleife liest die Datenblöcke in den Eingangspuffer mit readinto(), was Speicherallokationen vermeidet. Bei read_bytes = 0 wird das Dateiende erreicht. Der sample_count wird durch die Division der gelesenen Bytes durch 2 gerechnet, da jedes 16-Bit Sample 2 Bytes belegt. Nach der nativen Filterung wird der Ausgabepuffer in die Datei geschrieben, wobei write_mv[:read_bytes] sicherstellt, dass nur die gefilterten Bytes in die Ausgangsdatei geschrieben werden.

    # Header nachträglich korrigieren
    fout.seek(0)
    write_header(fout, frames)

Nach Abschluss der Verarbeitung wird der Header mit der korrekten Anzahl verarbeiteter Frames überschrieben. Dieser Schritt ist notwendig, da die finale Dateigröße erst nach vollständiger Verarbeitung bekannt ist. Mit seek(0) wird der Dateizeiger auf den Anfang der Header-Aktualisierung positioniert.

12 Echtzeit-Audiofilterung für Mikrofoneingang

Zur Demonstration der Echtzeitfilterung mit biquadratischen Filtern wird ein Mikrofonsignal digital gefiltert. Die Filterung wird mit einem ESP Lyrat 4.3 durchgeführt und mithilfe der audio-tools sowie den audio-board-driver Bibliotheken wird das Programm verfasst. Die Filter.h wurde für die Nutzung der transponierten Direktform 2 modifiziert, indem diese innerhalb des Bibliotheksverzeichnisses ausgetauscht wird.

12.1 Codeerklärung der Echtzeitfilterung

#include "AudioTools.h"
#include "AudioTools/AudioLibs/AudioBoardStream.h"

Für die Echtzeitfilterung werden die AudioTools.h und die AudioBoardStream.h eingebunden. Die AudioBoardStream.h ermöglicht einen I2S-Stream zwischen dem Audio-Codec des LyRaT mit dem ESP32 und die AudioTools ermöglichen die Verarbeitung von diesem Audiostream.

AudioInfo info(44100, 2, 16);
AudioBoardStream lyrat(LyratV43);
FilteredStream<int16_t, float> filtered(lyrat, info.channels);
StreamCopy copier(lyrat, filtered);

Die Audioparameter werden durch AudioInfo mit 44,1kHz, Stereo und 16-Bit definiert. Durch den Parameter LyratV43 in AudioBoardStream wird die Boardinitialisierung vorbereitet. Der gefilterte Stream filtered nutzt den lyrat Stream als Eingang und wird in Stereo gefiltert. Der StreamCopy copier übernimmt die kontinuierliche Übertragung der gefilterten Audiodaten vom Eingangssignal zur Audioausgabe des LyRaT.

const float b[] = {1.0, 0.0, 0.0};
const float a[] = {1.0, 0.0, 0.0};
const float gain = 1.0;

Die Filterkoeffizienten werden durch drei Arrays definiert. b[] stellt die Zählerkoeffizienten des Biquads dar und a[] enthält die Nennerkoeffizienten. Der Verstärkungsfaktor wird durch gain festgelegt. Mit diesen Werten wird der Filter implementiert, welcher den I2S-Stream verarbeiten soll.

void setup(void) {
    Serial.begin(115200);
    filtered.setFilter(0, new BiQuadTDF2<float>(b, a, gain));
    filtered.setFilter(1, new BiQuadTDF2<float>(b, a, gain));
    auto config = lyrat.defaultConfig(RXTX_MODE);
    config.input_device = ADC_INPUT_LINE1;
    lyrat.begin(config);
}

Die Setup-Funktion beginnt mit der Initialisierung der seriellen Kommunikation mit 115200 Baud. Anschließend wird der Audio-Stream des LyRaT mit der Standard-TX-Konfiguration initialisiert. Für beide Audiokanäle werden separate Biquad-Filter in transponierter Direktform 2 erstellt, wobei der linke Kanal über Index 0 und der rechte Kanal über Index 1 angesprochen wird. Der Audio-Stream des Lyrat wird initialisiert, wobei die Eingabequelle auf ADC_INPUT_LINE1 gesetzt wird, um die Onboard-Mikrofone als Audioquelle zu verwenden.

void loop() {
    copier.copy();
}

In der Loop-Funktion wird kontinuierlich copier.copy() aufgerufen, um die gefilterten Audiodaten vom Eingang zur Ausgabe zu übertragen und eine unterbrechungsfreie Echtzeit-Verarbeitung zu gewährleisten.

12.2 Filterkaskadierung

Die Filterkaskadierung erfolgt durch die serielle Anordnung mehrerer Filterstufen. Jede Stufe kann durch Biquad-Filter oder einzelne Sektionen einer SOS-Matrix realisiert werden.

filtered.setFilter(0, new FilterChain<float, 3>({
                      new BiQuadTDF2<float>(b, a, gain),
                      new BiQuadTDF2<float>(b, a, gain),
                      new BiQuadTDF2<float>(b, a, gain)
}));

filtered.setFilter(1, new FilterChain<float, 3>({
                      new BiQuadTDF2<float>(b, a, gain),
                      new BiQuadTDF2<float>(b, a, gain),
                      new BiQuadTDF2<float>(b, a, gain)
}));

Bei der Filterinstanziierung werden die Filterstufen mittels FilterChain<float, 3>definiert. Die einzelnen Biquad-Stufen können dabei entweder identische Koeffizienten verwenden oder unterschiedliche Koeffizientensätze erhalten, um Filter höherer Ordnung zu implementieren.

13 Praktische Anwendung der Bilinear-Transformation

Die analogen Biquad Filter für die Anwendung der Bilineartransformation werden aus dem Experiment 4 des Analog Systems Lab Kit PRO entnommen.

13.1 Übertragungsfunktionen der analogen Biquad Filter

Tiefpass: \(H_{TP}(s) = \frac{V_3}{V_i} = \frac{+H_0}{1 + \frac{s}{w_0Q} + \frac{s^2}{w_0^2}} = \frac{+H_0 \cdot w_0^2}{w_0^2 + \frac{sw_0}{Q} + s^2}\)

Hochpass: \(H_{HP}(s) = \frac{V_1}{V_i} = \frac{H_0 \cdot \frac{s^2}{w_0^2}}{1 + \frac{s}{w_0Q} + \frac{s^2}{w_0^2}} = \frac{+H_0 \cdot s^2}{w_0^2 + \frac{sw_0}{Q} + s^2}\)

Bandpass: \(H_{BP}(s) = \frac{V_2}{V_i} = \frac{-H_0 \cdot \frac{s}{w_0}}{1 + \frac{s}{w_0Q} + \frac{s^2}{w_0^2}} = \frac{-H_0 \cdot sw_0}{w_0^2 + \frac{sw_0}{Q} + s^2}\)

Bandsperre: \(H_{BS}(s) = \frac{V_4}{V_i} = \frac{(1 + \frac{s^2}{w_0^2 \cdot}) \cdot H_0}{1 + \frac{s}{w_0Q} + \frac{s^2}{w_0^2}} = \frac{(w_0^2 + s^2) \cdot H_0}{w_0^2 + \frac{sw_0}{Q} + s^2}\)

13.2 Analoge Filterschaltung

Analoge Biquad Schaltung

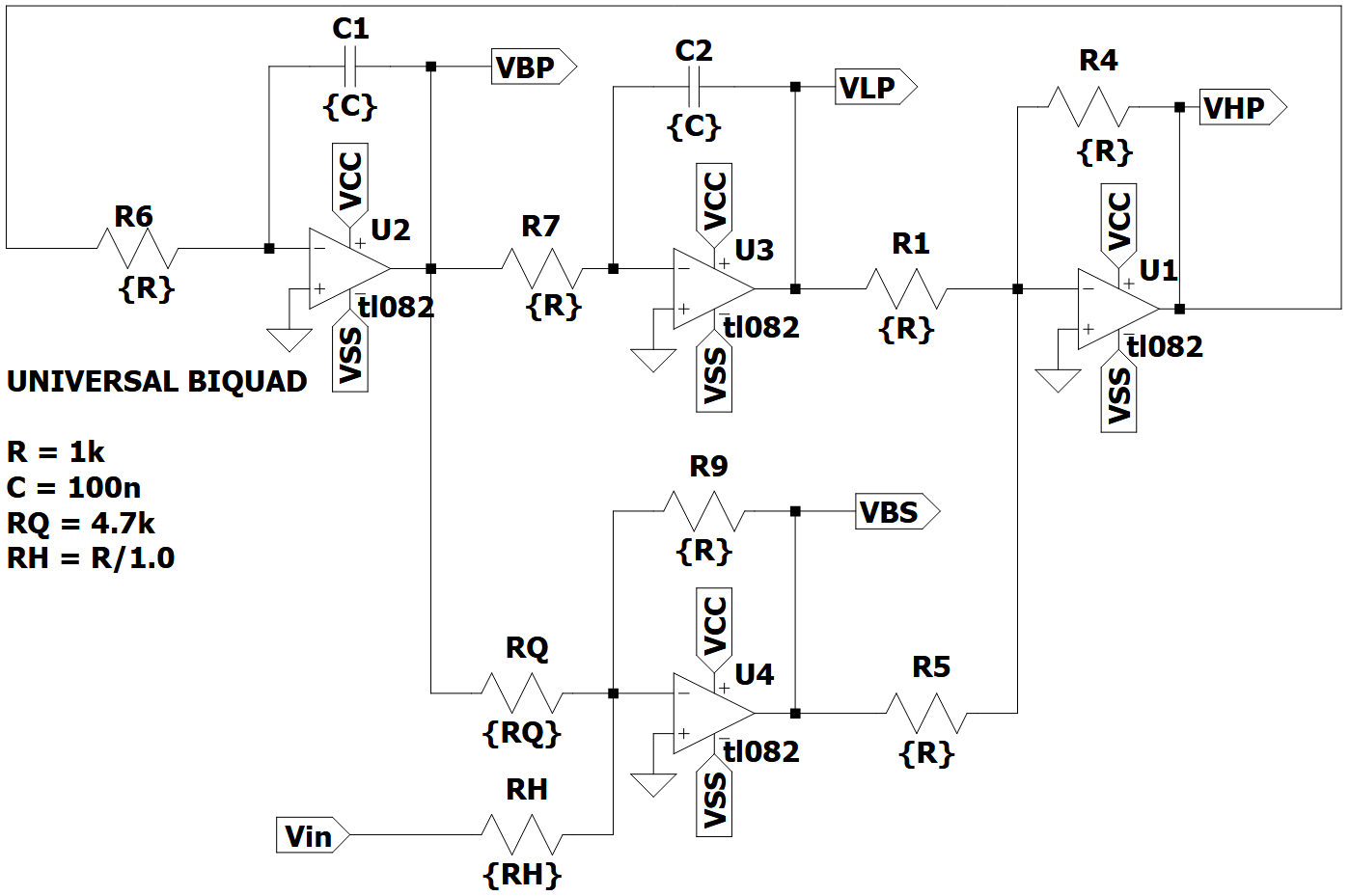
Um diese analogen Filter Bilinear zu transformieren stehen MATLAB sowie Python zur Verfügung, um die Durchführung der Substitutionen durchzuführen.

13.3 Python

Python mit scipy.signal

numz, denz = bilinear(nums ,dens ,fs = fs)
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import freqs, bilinear, freqz

Für die Bilinear-Transformation wird die Scipy-Bibliothek mit dem Signal-Modul verwendet. Aus diesem Modul werden die Funktionen freqs, bilinear und freqz importiert. Für weitere Berechnungen wird Numpy als np importiert und für die Möglichkeit zum Plotten wird Matplotlib.pyplot als plt importiert.

R = 1000
C = 100e-9
w0 = 1 / (R * C)
Q = 4.7
fs = 44100

Aus dem Schaltbild der analogen Filterschaltung werden dessen Parameter entnommen. Die Kreisfrequenz \(w_0\) berechnet sich durch \(w_0 = \frac{1}{R C}\). Der Wert \(H_0\) beschreibt den Gainfaktor der Filterschaltungen und wird auf 1 gesetzt, wodurch dieser nicht mehr im Code aufkommt. Die digitalen Filter sollen für Audioanwendungen verwendet werden, weshalb die Wahl von 44,1 kHz als Abtastfrequenz getroffen wurde. Durch die Wahl der Abtastefrequenz von 44,1 kHz wird kein Prewarping benötigt, da die Frequenzverzerrung vernachlässigbar ist.

# Tiefpass Zähler
TP_nums = [0, 0, w0**2]

# Hochpass Zähler
HP_nums = [1, 0, 0]

# Bandpass Zähler
BP_nums =  [0, -w0, 0]

# Bandstop Zähler
BS_nums = [1, 0, w0**2]

# Nenner
dens = [1, w0/Q, w0**2]

Die Zähler und Nenner der Übertragungsfunktionen der analogen Filter werden als Listen übernommen. Die Listenelemente entsprechen den Koeffizienten in absteigender Potenzordnung: \([s^2, s^1, s^0]\). Die Nenner der vier Filter sind identisch und müssen nur einmal übernommen werden.

# Bilineartransformation

# Tiefpass
TP_numz, TP_denz = bilinear(TP_nums, dens, fs = fs)

# Hochpass
HP_numz, HP_denz = bilinear(HP_nums, dens, fs = fs)

# Bandpass
BP_numz, BP_denz = bilinear(BP_nums, dens, fs = fs)

# Bandstop
BS_numz, BS_denz = bilinear(BS_nums, dens, fs = fs)

Die Bilineartransformation wird durch bilinear durchgeführt, indem dieser Funktion die Zähler- und Nennerlisten der jeweiligen Filter mit der Abtastfrequenzen \(f_s\) übergeben werden. Die Funktion liefert die Zähler- und Nennerkoeffizienten der digitalen Übertragungsfunktion.

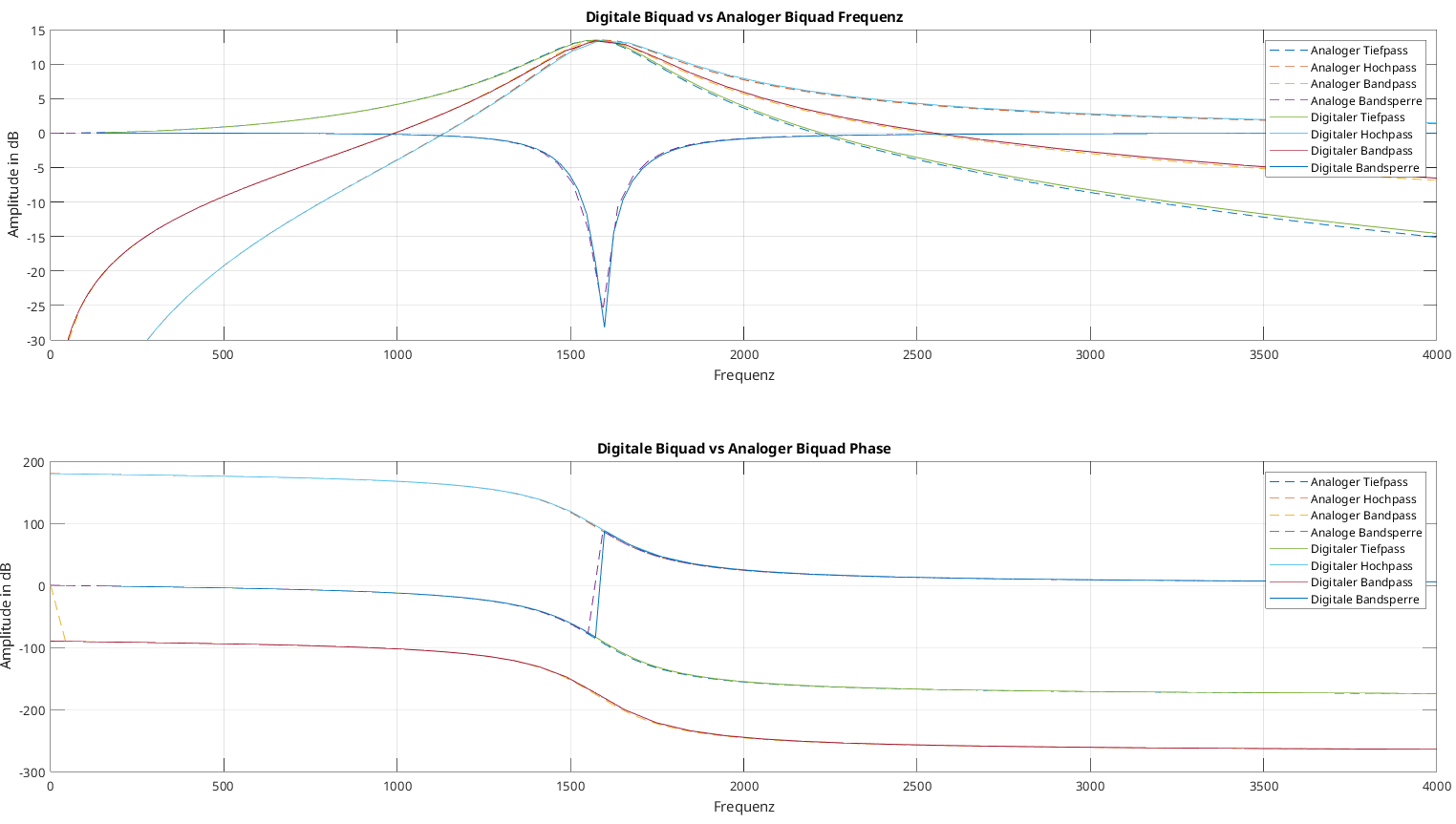
Vergleich zwischen analogen und digitalen Frequenz- und Phasengang

14 Filterentwurf in Python

Für den Entwurf von digitalen IIR-Filtern wird in Python die Scipy-Bibliothek mit dem Signal-Modul verwendet. Diese Bibliothek bietet über eine umfassende Sammlung von Funktionen für den Entwurf und die Analyse von digitalen Filtern. Für den Entwurf von digitalen Biquad-Filtern wird das Entwurfsverfahren mit analogem Prototyping durchgeführt.

from scipy.signal import butter, cheby1, cheby2, ellip

Das Entwurfsverfahren basiert auf der Transformation analoger Filterprototypen, bei welchem ein analoger Filter mit den gewünschten Eigenschaften entworfen wird und anschließend durch die Bilineartransformation mit Prewarping in den digitalen Bereich überführt wird.

Zur beispielhaften Nutzung der Funktionen werden die vier Grundfiltertypen nach den folgenden Parametern entworfen:

# Ordnung für Tief- und Hochpass
order = 4
# Ordnung für Bandpass und Bandsperre
order_b = 2

Zur Demonstration werden Filter vierter Ordnung entworfen, um die Unterschiede zwischen der Filterprotypen zu verdeutlichen.

Für den Entwurf von biquadratischen Tief- und Hochpass-Filter wird die Ordnung auf den Wert 2 gesetzt. Bei Bandpass und Bandsperr-Filtern muss die Ordnung auf 1 gesetzt werden, um einen biquadratischer Filter zu erhalten.

Beim Entwurf von Bandpass- und Bandsperr-Filtern wird eine Frequenztransformation eines Tiefpass-Prototyps durchgeführt, bei welcher jede s-Variable quadriert wird, wodurch sich die Filterordnung automatisch verdoppelt.

# Abtastrate für Audioanwendungen in Hz - Standard für CD-Qualität
fs = 44100
# Grenzfrequenz für Tief- und Hochpass in Hz
fc = 1000
# Normalisierte Grenzfrequenz
wn = fc/(fs/2)
# Untere und obere Grenzen für Bandpass und Bandsperre in Hz
low = 500
high = 2000
# Normalisierte untere und obere Grenzen
wn_b = [low/(fs/2), high/(fs/2)]
# Welligkeit(Ripple) im Durchlassbereich in dB
rp = 0.5
# Dämpfung im Sperrbereich in dB
rs = 80

Über die Funtkionen butter, cheby1, cheby2 und ellip werden die dementsprechenden Filter enworfen. Über den Parameter btype wird entschieden, welcher Filtertyp entworfen wird durchs Einsetzen von low, high, bandpassund bandstop.

Die Koeffizienten können als separate b und a Arrays oder als eine Second Order System (SOS)-Matrix durch output = 'sos' ausgegeben werden. Mit der SOS-Matrix bietet sich die Möglichkeit auch Filter höherer Ordnung, als kaskadierte Biquad-Sektionen zu realisieren. Für den Entwurf von digitalen Filtern wird beim Parameter analog = False gesetzt.

Mit dem Parameter rp lässt sich die Welligkeit (Ripple) im Durchlassbereich von Chebyshev1- und Elliptischen Filtern kontrollieren und mit dem Parameter rs die Dämpfung im Sperrbereich von Chebyshev2- und Elliptischen Filtern.

Butterworth-Filter

Der Butterwoth-Filter zeichnet sich aus mit seiner maximalen Flachheit im Durchlassbereich ohne Welligkeit aus. Als Kompromiss weist dieser einen relativ langsamen Übergang vom Durchlass- zum Sperrbereich auf. Er bietet ein ausgewogenes Verhältnis zwischen Phasenverhalten und Flankensteilheit.

b, a = butter(N = order, Wn = wn, btype = 'low', analog = False)
b, a = butter(N = order, Wn = wn, btype = 'high', analog = False)
sos = butter(N = order_b, Wn = wn_b, btype = 'bandpass',
             analog = False, output = 'sos')
sos = butter(N = order_b, Wn = wn_b, btype = 'bandstop',
             analog = False, output = 'sos')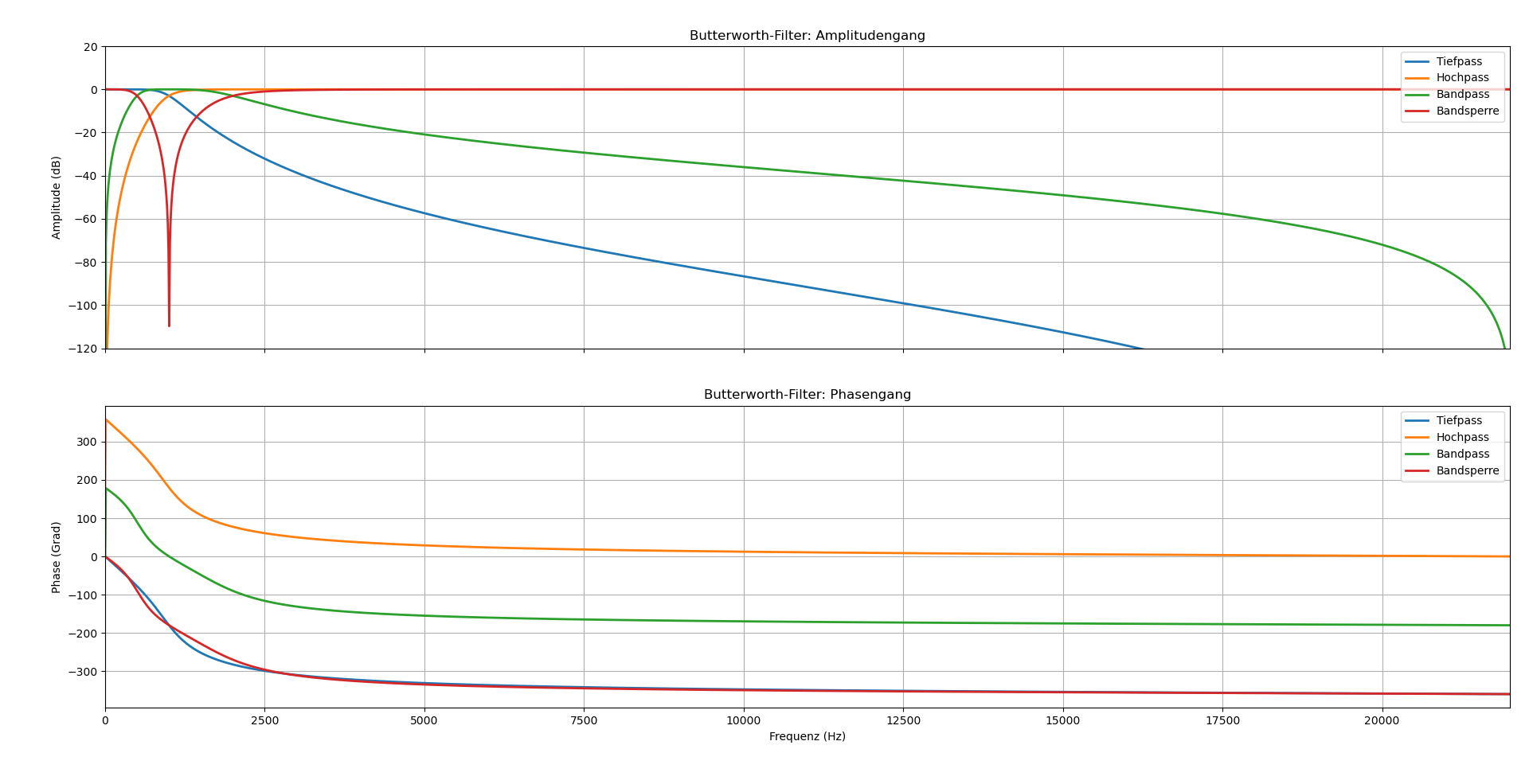

Butterworth-Filter

Chebyshev Typ 1-Filter

Der Chebyshev Typ 1-Filter weist Welligkeit im Durchlassbereich auf, ermöglicht jedoch einen steileren Übergang im Vergleich zum Butterworth-Filter. Die Wellikgkeit ist gleichmäßig über den gesamten Durchlassbereich verteilt.

b, a = cheby1(N = order, rp = rp,Wn = wn, btype = 'low', analog = False)
b, a = cheby1(N = order, rp = rp, Wn = wn, btype = 'high', analog = False)
sos = cheby1(N = order_b, rp = rp, Wn = wn_b, btype = 'bandpass',
             analog = False, output = 'sos')
sos = cheby1(N = order_b, rp = rp, Wn = wn_b, btype = 'bandstop',
             analog = False, output = 'sos')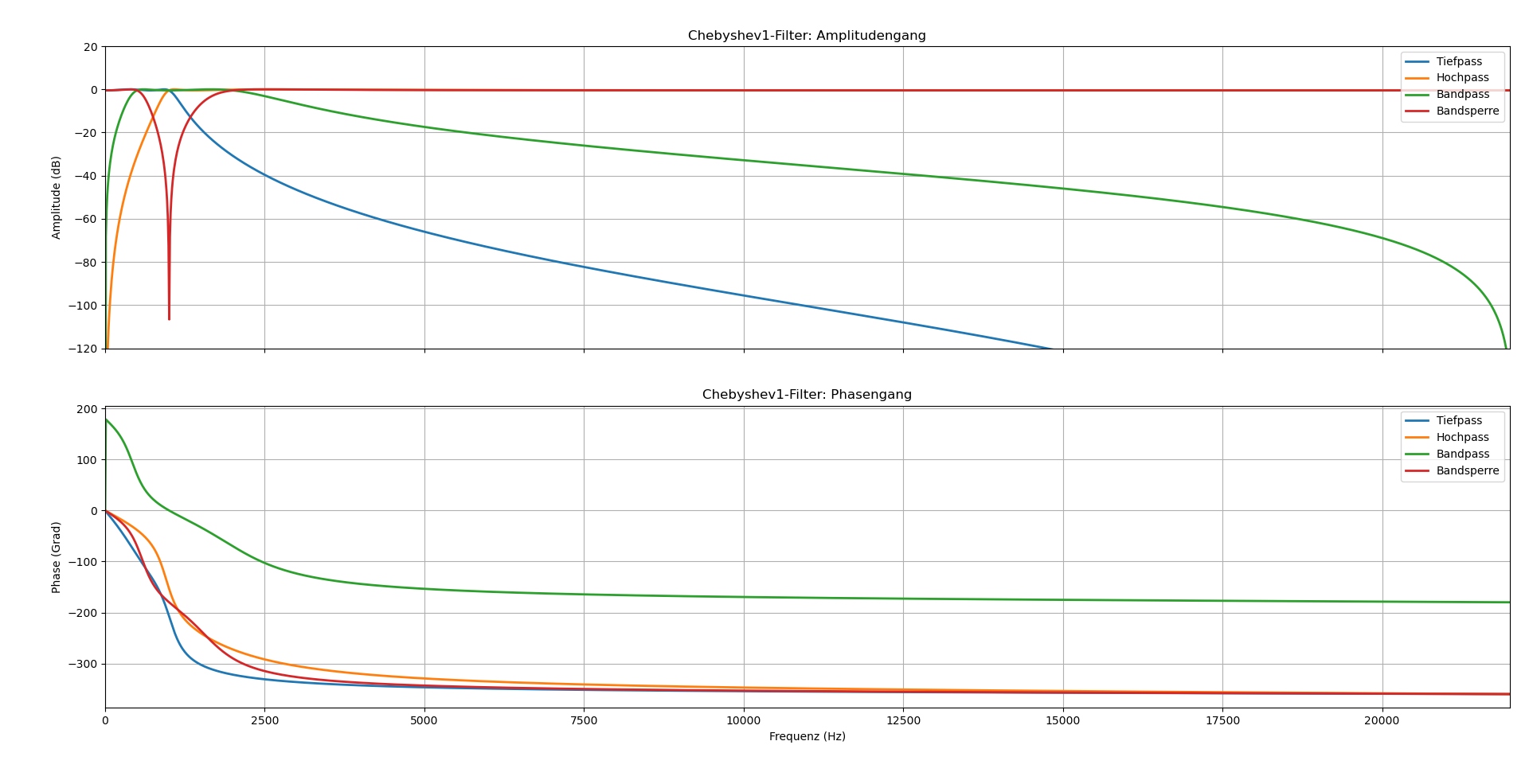

Chebyshev1-Filter

Chebyshev Typ 2-Filter

Der Chebyshev Typ 2-Filter kombiniert einen flachen Durchlassbereich, vergleichbar mit dem Butterworth-Filter, mit Welligkeit im Sperrbereich. Bei gleichmäßiger Sperrbereichsdämpfung ermöglicht dieser steile Übergangsflanken.

b, a = cheby2(N = order, rs = rs,Wn = wn, btype = 'low', analog = False)
b, a = cheby2(N = order, rs = rs, Wn = wn, btype = 'high', analog = False)
sos = cheby2(N = order_b, rs = rs, Wn = wn_b, btype = 'bandpass',
             analog = False, output = 'sos')
sos = cheby2(N = order_b, rs = rs, Wn = wn_b, btype = 'bandstop',
             analog = False, output = 'sos')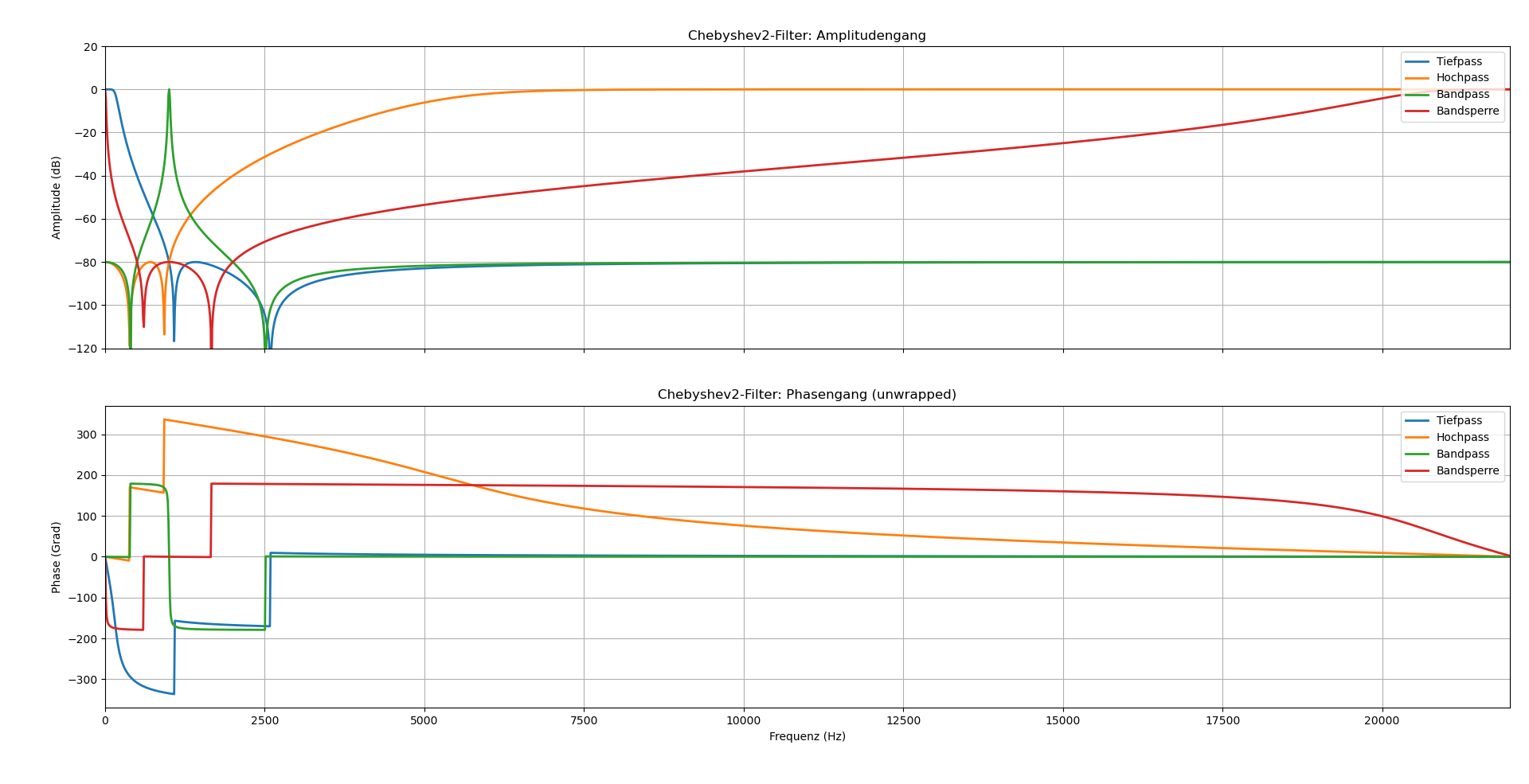

Chebyshev2-Filter

Elliptischer Filter (Cauer)

Der elliptische Filter bietet die steilsten Übergangsflanken aller dargestellten Filtertypen, weist jedoch Welligkeiten sowohl im Durchlass- als auch im Sperrbereich auf. Dieser eignet sich Optimal für Anwendungen mit strengen Anforderungen an die Übergangsanforderungen.

b, a = ellip(N = order, rp = rp, rs = rs,Wn = wn, btype = 'low', analog = False)
b, a = ellip(N = order, rp = rp, rs = rs, Wn = wn, btype = 'high', analog = False)
sos = ellip(N = order_b, rp = rp,  rs = rs, Wn = wn_b, btype = 'bandpass',
            analog = False, output = 'sos')
sos = ellip(N = order_b, rp = rp,  rs = rs, Wn = wn_b, btype = 'bandstop',
            analog = False, output = 'sos')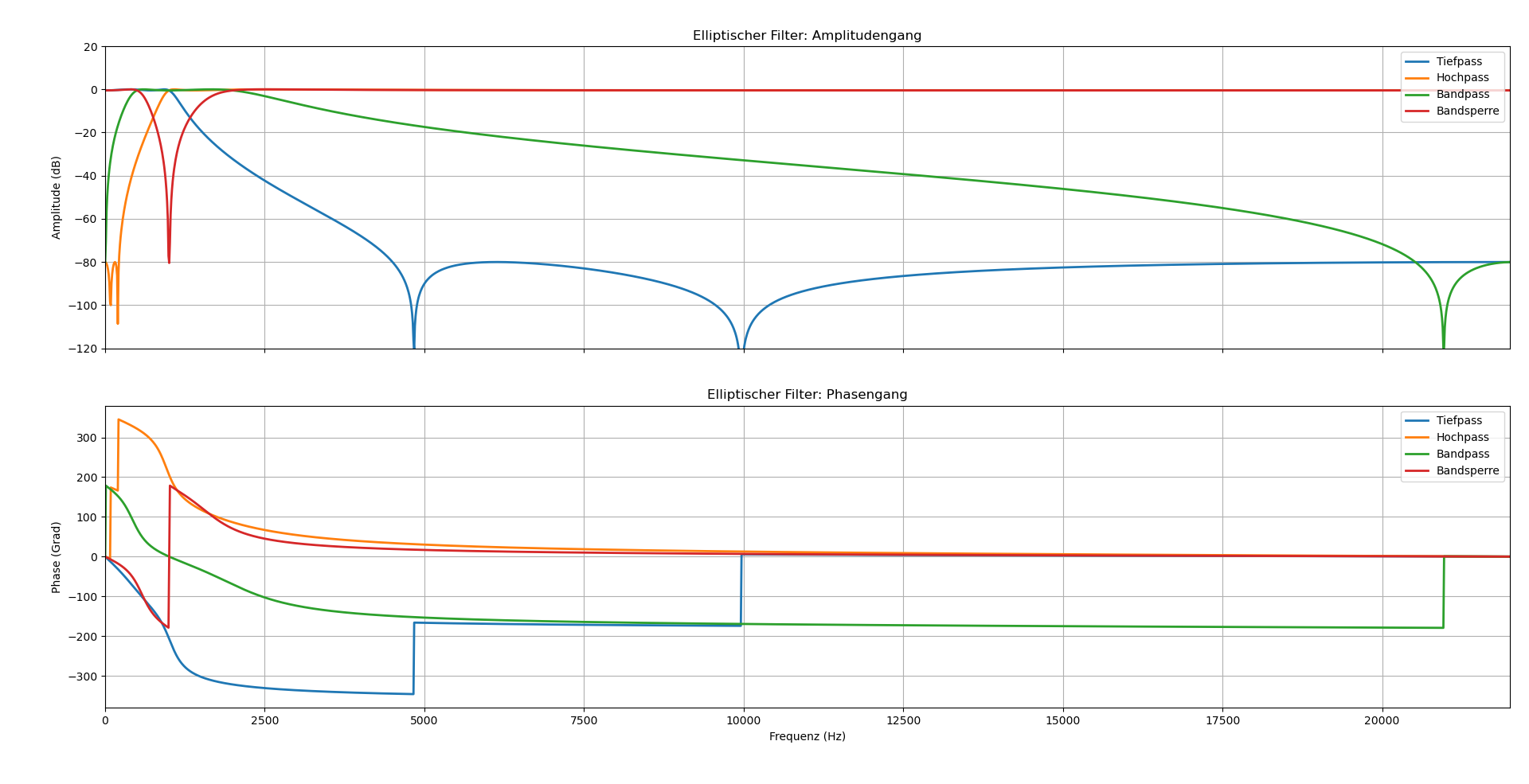

Elliptischer Filter

Das Notebook filter_desing.ipynb ermöglicht eine Vergleichsanalyse der verschiedenen Entwurfsmethoden unter indentischen Parametern und bietet eine Basis für die Filterauswahl basierend auf den spezifischen Anwendungsanforderungen.

15 Pyfda - Pythonfilterdesigntool

Pyfda (Python Filter Design and Analysis) ist ein Open-Source-Tool, das als grafische Benutzeroberfläche für den Entwurf und die Analyse digitaler Filter entwickelt wurde. Die Anwendung basiert auf den Python-Bibliotheken PyQt5, NumPy, SciPy sowie Matplotlib und bietet Funktionalitäten, die dem Filter Design Tool in MATLAB ähneln.

Die Installation von Pyfda erfolgt über den Python Package Manager:

pip install pyfda

Das Tool wird anschließend mittels des Befehls pyfdax gestartet.

15.1 Demonstrativer Filterentwurf mit Frequenzgangbetrachung

Für die vorliegende Arbeit wurde ein Bandpassfilter 6. Ordnung mit einem Durchlassbereich von 300 Hz bis 3400 Hz entworfen. Diese Spezifikation entspricht dem Frequenzbereich der menschlichen Sprache und ist daher für Audioanwendungen von besonderer Relevanz.

Als Filterprototyp wurde ein elliptischer Filter (Cauer-Filter) gewählt, da dieser durch seine äqui-ripple-Charakteristik sowohl im Durchlass- als auch im Sperrbereich die steilsten Übergänge bei gegebener Filterordnung ermöglicht. Die Entwurfsparameter wurden wie folgt festgelegt:

  • Welligkeit im Durchlassbereich: rp = 0.5 dB
  • Dämpfung im Sperrbereich: rs = 90 dB
  • Durchlassbereich: 300 Hz - 3400 Hz

Pyfda: Entwurfsparameter
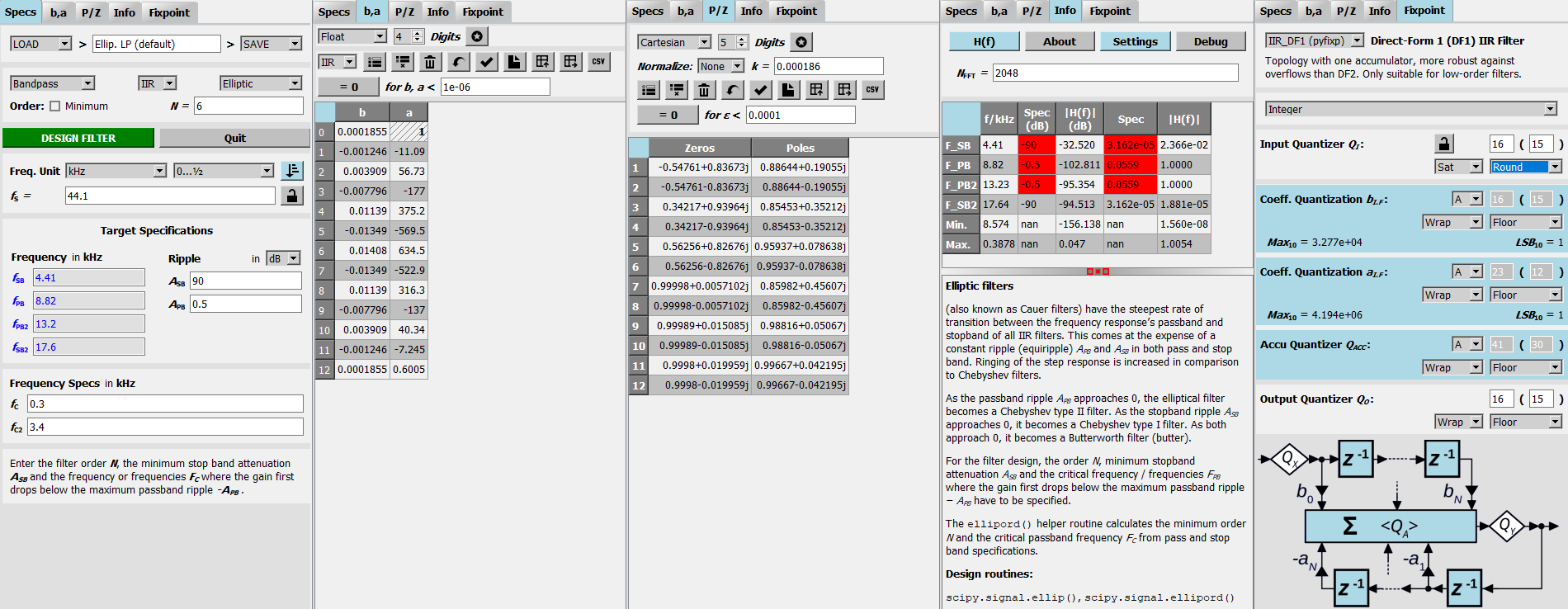
Specs b, a P/Z Info Fixpoint
Spezifikation der Filterparamtern und des Entwurfsverfahrens. Ausgabe der b- und a-Koeffizienten. Ausgabe der Pole und Nullstellen. Frequenzanalyse, Parameterauflistung sowie Beschreibung des Filtertyps. Konvertierung zur Festkomma-Quantisierung für die Direktform 1.

Pyfda: Analyseplots
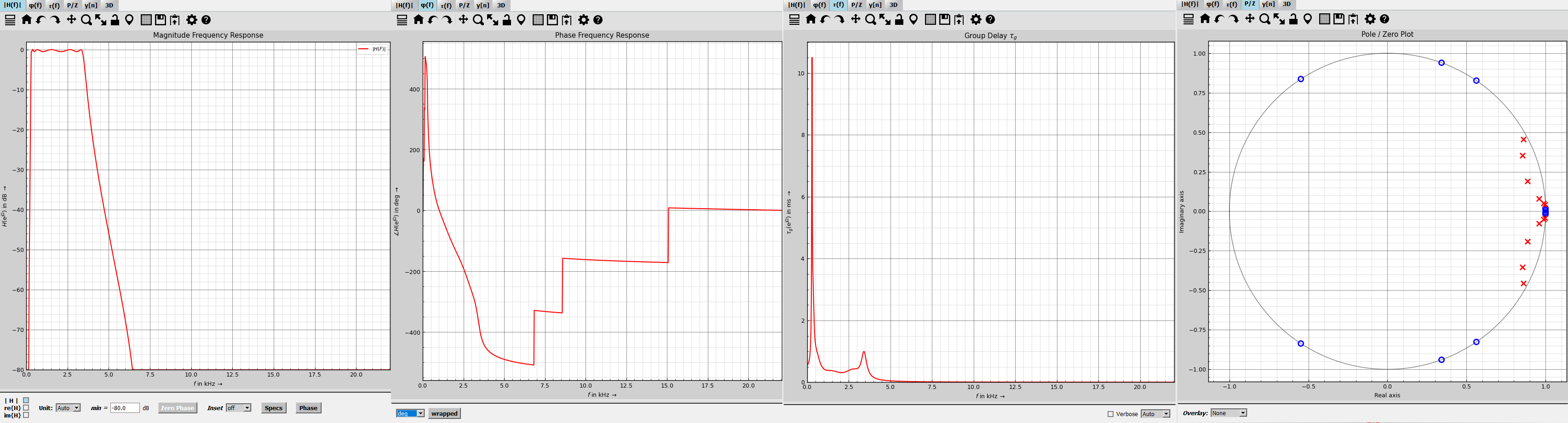
Magnitude Response Phase Response Group Delay Pole-Zero Plot
Zeigt den Betrag der Übertragungsfunktion \(|H(f)|\) in dB. Zeigt die Phase von \(H(f)\) über der Frequenz. Zeigt die Gruppennachlaufzeit \(\tau_g\) an. Zeigt die Pole (×) und Nullstellen (○) in der z-Ebene.

Obwohl Pyfda umfassende Entwurfs- und Analysemöglichkeiten bietet, beschränkt sich der Export auf die b- und `ae-Koeffizienten sowie die Pol- und Nullstellen. Für die Implementierung auf Mikrocontrollern wird jedoch eine (Second-Order-Sections) SOS-Matrix benötigt, die eine numerisch stabilere Darstellung des Filters ermöglicht.

sos = ellip(N = 6, 
            rp = 0.5, 
            rs = 90, 
            Wn = [300/(44100/2], 3400/(44100/2)]
            btype = 'bandpass', 
            analog = False,
            output = 'sos')

Diese SOS-Matrix kann anschließend in die entsprechenden Arduino-Implementierungen (filter_wav_casceded.ino oder filter_microphone_cascaded.ino) integriert werden.

Zur Veranschaulichung der Filterwirkung wurden Jupyter Notebooks entwickelt, die im Verzeichnis filter_demonstration/visual/ verfügbar sind. Diese ermöglichen die Visualisierung von den Frequenzgängen sowohl der WAV-Dateien als auch der Echtzeitübertragung.

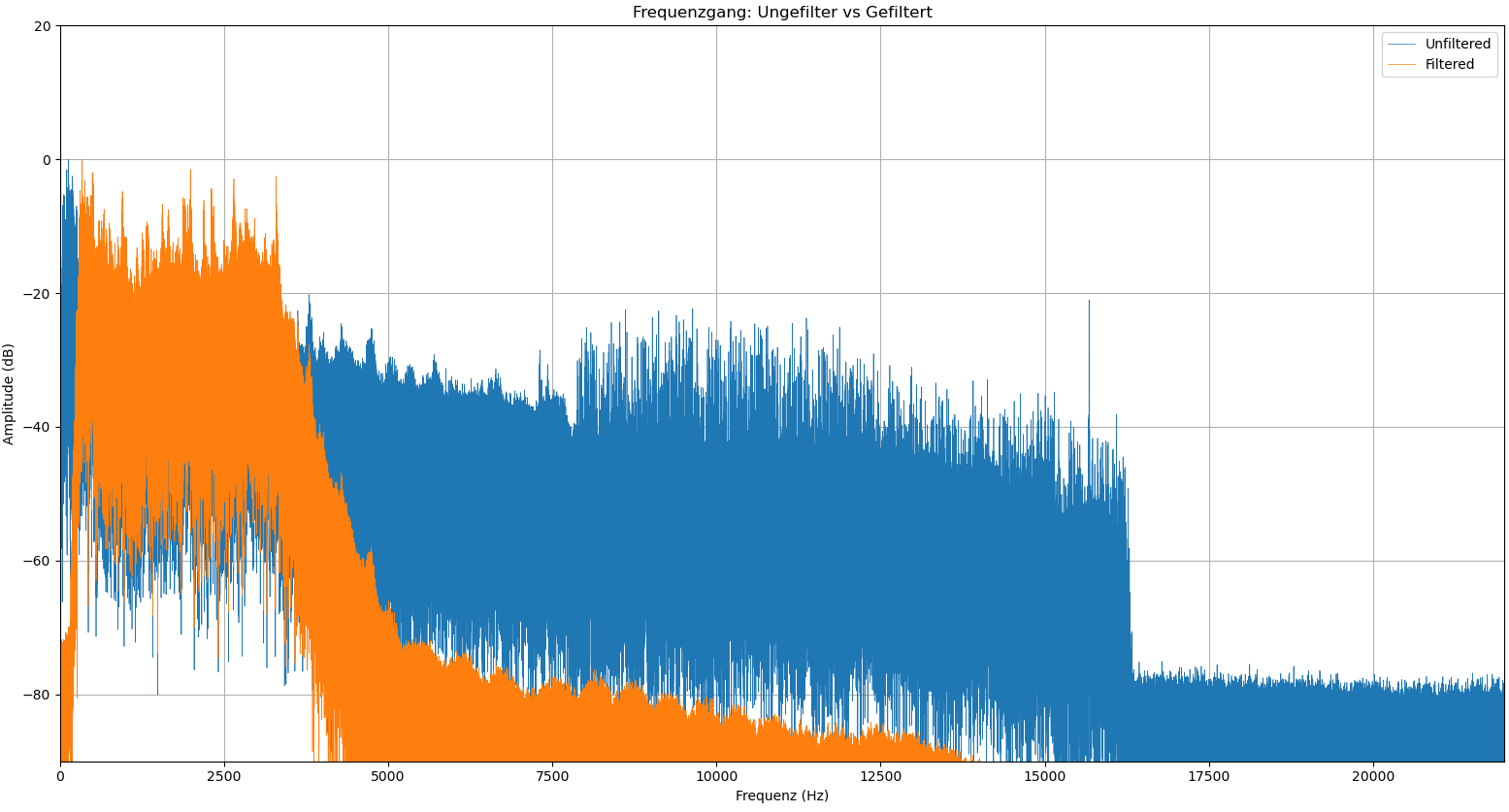
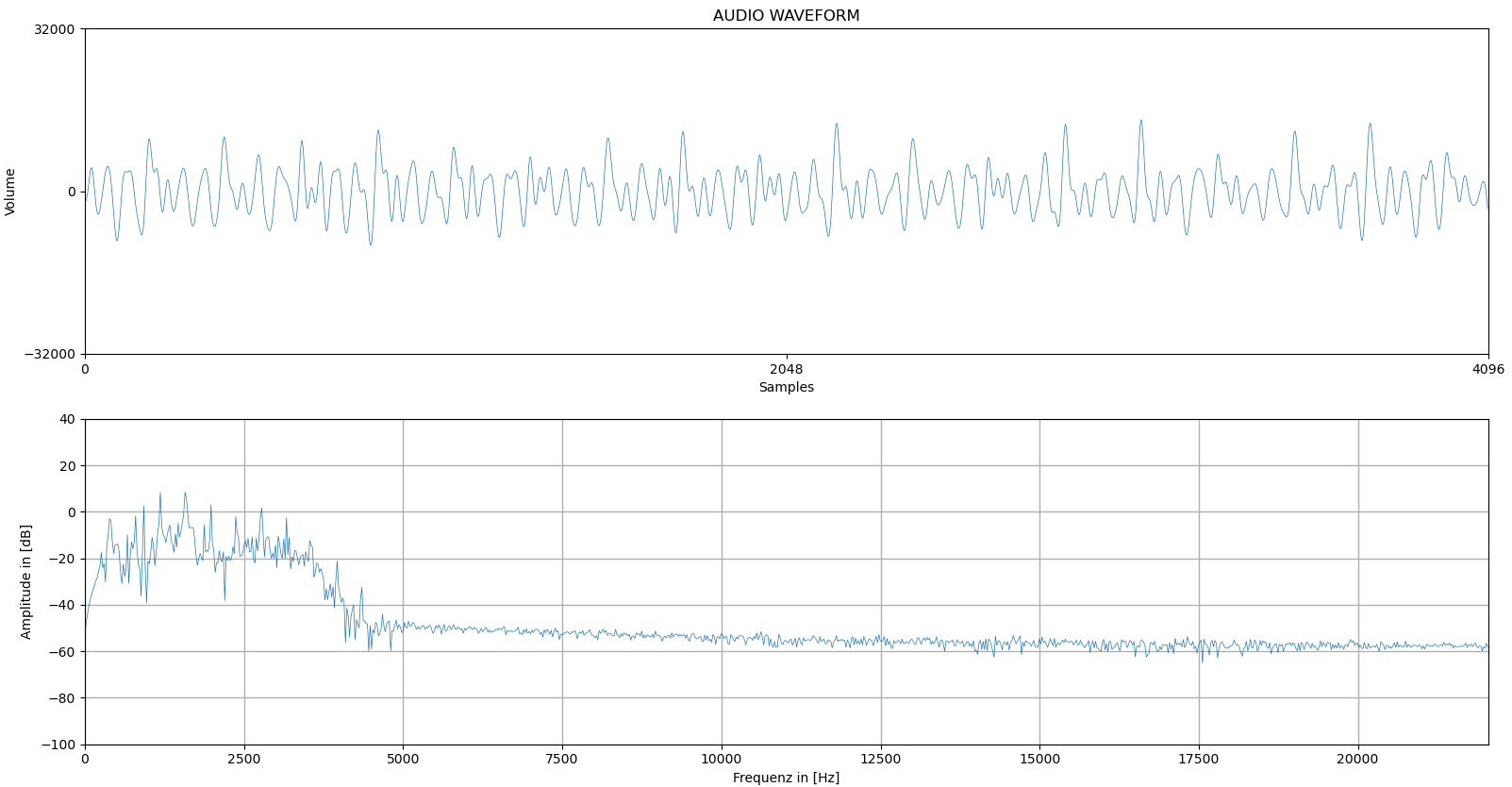
Ungefiltert und Gefilterte Visualisierung Echtzeit-Visualisierung

16 Evaluierung der Filterimplementierung auf Mikrocontrollern

16.1 Zielsetzung der Evaluierung

Ziel dieses Kapitels ist es, die praktische Umsetzung der digitalen Biquad-Filter hinsichtlich Verarbeitungsdauer, Strukturauswahl, Stabilität und Echtzeitfähigkeit systematisch zu bewerten. Dabei wird insbesondere der Vergleich zwischen MicroPython und Arduino untersucht. Darüber hinaus werden die verschiedene Filterstrukturen (Direktform 1, Direktform 2, transponierte Direktform 2) auf derselben Hardware verglichen. Abschließend wird die Verarbeitung eines IIR-Filters höherer Ordnung (6. Ordnung) implementiert und verarbeitet, um die Skalierbarkeit der Implementierung zu bewerten.

16.2 Testumgebung

Die Evaluierung wurde auf dem ESP32 basierten Lyrat V4.3 durchgeführt. Als Eingangssignal diente eine WAV-Datei mit folgenden Eigenschaften:

  • Dateiname: TF2_theme.wav
  • Länge: 1 Minute 12 Sekunden (72 Sekunden)
  • Abtastrate: 44,1 kHz
  • Bittiefe: 16 Bit
  • Kanäle: Stereo
  • Gesamte Sample-Anzahl: 3.215.360

Das Audiosignal wurde vollständig geladen und jeweils kanalweise (links/rechts) durch einen digitalen Filter verarbeitet. Die Messung der Laufzeit erfolgte mit time.ticks_ms() unter MicroPython. Für Vergleichbarkeit wurden je fünf Durchläufe pro Konfiguration durchgeführt.

16.3 Vergleich der TDF2: MicroPython vs. Arduino

Für den ersten Benchmark wurde eine Bandsperre zweiter Ordnung mit folgenden Designparametern implementiert:

  • Filterart: IIR-Biquad (Bandsperre)
  • Fs: 44,1 kHz
  • low cutoff: 1250 Hz
  • high cutoff: 1450 Hz
  • Koeffizienten:
  • b = [0.07033, -0.1380, 0.07033]
  • a = [1.00000, -0.1380, -0.8593]

Dieser Filter wurde geziehlt grenzstabil Entworfen, um einen Vergleich zwischen der Stabilität der Strukturen zu Vergleichen.

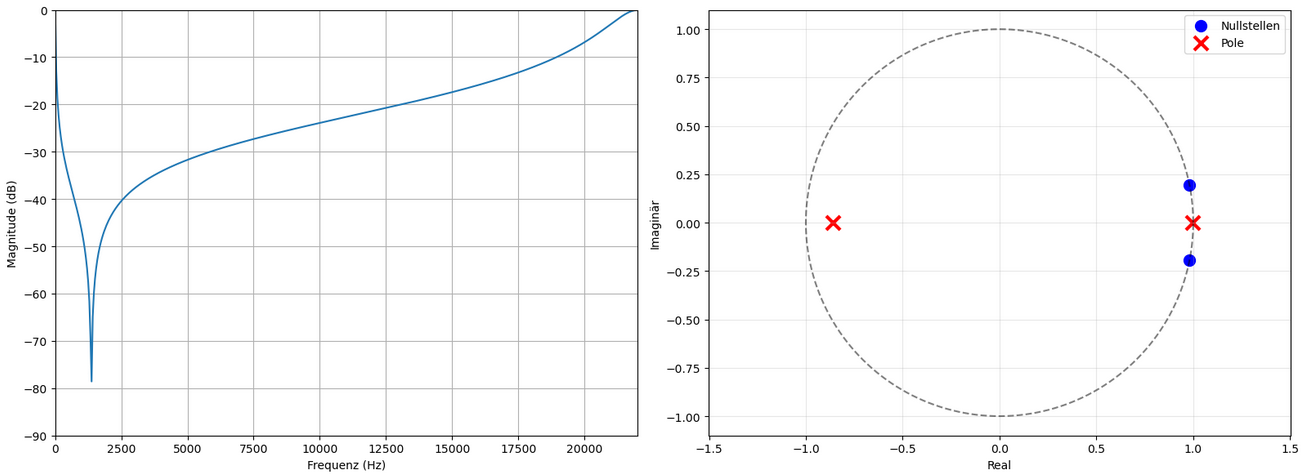
Frequenzgang und Pol- und Nullstellen von der Bandsperre

16.3.1 Verarbeitungsdauer

Plattform Struktur Durchschnittliche Dauer Spanne
MicroPython TDF2 549,27s 548,66 – 550,69s
Arduino (C++) TDF2 16,60s 16,48 – 16,97s

16.3.2 Interpretation

Die Ergebnisse zeigen eine massive Performance-Differenz zwischen den beiden Umgebungen: Die Arduino-Variante ist über 33-mal schneller als die MicroPython-Variante. Während die interpretierte Ausführung von MicroPython für einfache Skripte ausreichend ist, erweist sie sich bei Sample-genauer Signalverarbeitung als ungeeignet für Echtzeitanwendungen. Arduino bietet hingegen eine echtzeitnahe Ausführung mit direktem Hardwarezugriff und optimierter Kompilierung, wodurch die Umsetzung effizient und praxisnah gelingt.

16.4 Vergleich verschiedener Filterstrukturen auf Arduino

16.4.1 Übersicht der Filterstrukturen

  • Direktform 1 (DF1): Klassische Struktur mit separater Verarbeitung von x[n] und y[n].
  • Direktform 2 (DF2): Speicheroptimierte Version mit gleichem Output, aber reduzierter Verzögerung.
  • Transponierte Direktform 2 (TDF2): Numerisch stabilere Variante von DF2.

16.4.2 Verarbeitungszeitmessungen (Arduino)

Struktur Verarbeitungszeiten (s) Durchschnitt
TDF2 16,55 – 16,97 16,60
DF2 16,72 – 16,84 16,78
DF1 16,42 – 16,91 16,53

16.4.3 Funktionalität und Stabilität

DF2-Filterverlauf

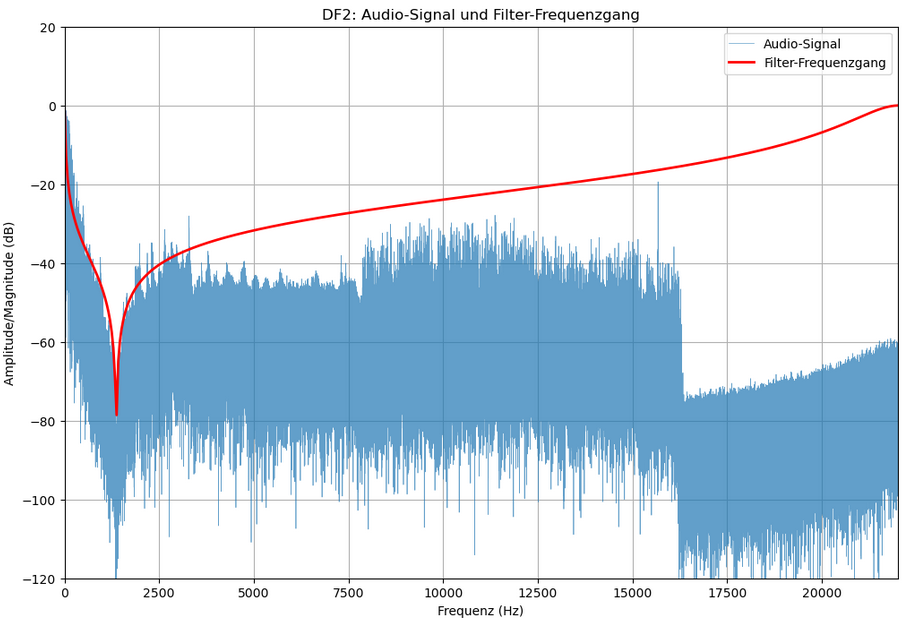
Die Implementierungen von TDF2 und DF2 zeigten eine korrekte und deutlich wahrnehmbare Filterwirkung.

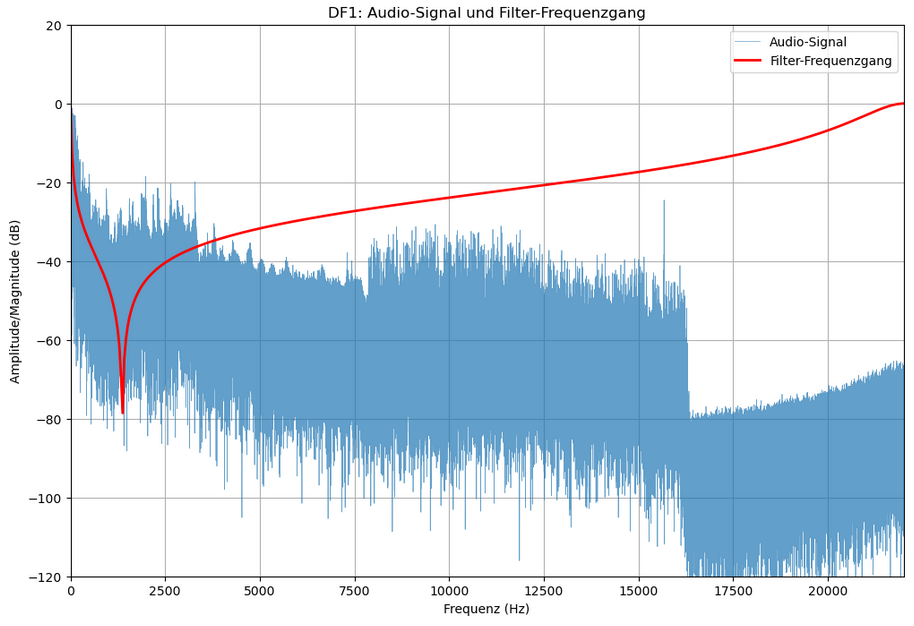DF1-Filterverlauf Die Implementierung mit DF1 führte hingegen nur zu einer minimalen Dämpfung, welche nicht dem Sperrbereich der Bandsperre entspricht. Eine Ursache könnte darin liegen, dass die Pole des Filters sehr nahe am Einheitskreis liegen. In Direktform 1 kann dies zu numerischer Instabilität und unzureichender Dämpfung führen, insbesondere bei Float-basierten Mikrocontrollerumgebungen mit begrenzter Genauigkeit.

16.4.4 Fazit Strukturen

Struktur Durchschnitt (s) Filterwirkung Bewertung
TDF2 16,60 Eindeutig, stabil Empfohlen für Echtzeitanwendung
DF2 16,78 Eindeutig, stabil Ebenfalls gut geeignet
DF1 16,53 Nur leichte Dämpfung Nicht geeignet bei kritischen Filtern

16.5 Erweiterung: Filterung mit sechster Ordnung (6 Biquad-Segmente in Kaskade)

16.5.1 Koeffizienten der Kaskade

Der entworfene Filter aus der PyFDA-Demonstration wurde für die Verarbeitszeitmessung zum Vergleich zwischen einfachen Biquads verwendet. Der Filter ist ein elliptischer Bandpass 6. Ordnung, wodurch die Filterung durch sechs Segmente ausgeführt wird.

Section 1: [b0, b1, b2, a0, a1, a2]
Section 2: [...]
...
Section 6: [...]

16.5.2 Ergebnisse (Arduino TDF2, 6 Biquad-Sektionen)

Lauf Dauer (s)
1 23,50
2 23,47
3 23,45
4 23,48
5 23,43
Ø 23,47

16.5.3 Beobachtungen

  • Im Vergleich zum einem einzelnen Biquad (16,60s) liegt die Verarbeitungszeitsteigerung bei ca. 41%.
  • Dies entspricht einer annähernd linearen Skalierung pro zusätzlicher Biquad-Stage.
  • Auch bei höherer Ordnung bleibt der Filter echtzeitfähig und speichereffizient.

16.6 Zusammenfassung der Evaluierung

Aspekt MicroPython Arduino C++ (ESP32)
Filtergeschwindigkeit Extrem langsam Echtzeitnah (16s)
Strukturauswahl Nur TDF2 praktikabel TDF2 > DF2 > DF1
Stabilität (DF1) n/a Eingeschränkt bei bestimmten Koeffizienten
Erweiterbarkeit (Kaskade) Ungeeignet Problemlos bis ≥ 6. Ordnung
Entwicklungsaufwand Gering Mittel (C++)
Geeignet für Praxis? Nein Ja

Die durchgeführten Benchmarks bestätigen, dass die Implementierung digitaler Biquad-Filter auf dem ESP32 mit Arduino vollständig praxistauglich und echtzeitfähig ist. MicroPython hingegen ist für performante Audiobearbeitung ungeeignet, kann aber zum schnellen Prototyping sinnvoll sein. Die transponierte Direktform 2 stellt sich als beste Struktur durch ihre effizienz, stabilität und leichte skalierbarkeit heraus. Die erfolgreiche Anwendung eines Filters sechster Ordnung belegt zudem, dass auch komplexere Designs zuverlässig auf der Zielhardware ausführbar sind.

17 Gegenüberstellung von Mikrocontroller und FPGA Implementierung

Parallel zu dieser Bachelorarbeit wurde eine weitere Arbeit mit ähnlicher Fragestellung durchgeführt. Beide Arbeiten beschäftigen sich mit der praktischen Umsetzung digitaler IIR-Filter, unterscheiden sich jedoch grundlegend in der gewählten Implementierungsplattform. Während sich die eine Arbeit auf die softwarebasierte Realisierung mit FPGA konzentriert, steht in dieser Arbeit die softwarebasierte Realisierung mit Mikrocontrollern im Mittelpunkt.

Die Mikrocontroller-Implementierung erfolgt direkt in Arduino bzw. MicroPython. Die Biquad-Filter werden dabei auf Basis ihrer Differenzengleichungen manuell in Code umgesetzt. Verschiedene Strukturformen wie Direktform 1, Direktform 2 und deren transponierte Variante (TDF2) wurden explizit implementiert. Besonderheiten wie die manuelle Verwaltung interner Zustände oder Verzögerungsglieder sowie Optimierungen (z. B. durch __slots__ in MicroPython oder native Kompilierung einzelner Methoden) tragen zur Effizienzsteigerung bei.

Während Arduino eine vergleichsweise leistungsstarke Umsetzung ermöglicht und eine Echtzeitverarbeitung über die I2S-Schnittstelle grundsätzlich mittles vorhandener Bibliotheken ermöglicht, ist MicroPython aufgrund seiner Interpreterstruktur deutlich langsamer. Zusätzlich verhinderten fehlende I2S-Treiber in MicroPython eine Audioverarbeitung in Echtzeit. Daher beschränkte sich die MicroPython-Implementierung auf die Filterung zuvor gespeicherter WAV-Dateien.

Im Gegensatz dazu basiert die FPGA-Implementierung auf einem modellbasierten Entwicklungsansatz mittels MATLAB/Simulink und dem HDL Coder. Die Filterstrukturen, insbesondere Direct Form II transponiert mit Pipelining, werden als Simulink-Modelle aufgebaut und anschließend in synthesefähigen VHDL-Code überführt. Die resultierenden IP-Cores werden über AXI4-Stream-Schnittstellen in ein Vivado-Projekt eingebunden. Die Verarbeitung erfolgt hardwareseitig, was eine hohe Parallelität und Echtzeitfähigkeit erlaubt. Die PYNQ-Plattform ermöglicht darüber hinaus eine komfortable Steuerung und Visualisierung über Jupyter Notebooks mit Python. Ein geplanter Echtzeitbetrieb über die I2S-Schnittstelle des integrierten Audio-Codecs ADAU1761 konnte jedoch aufgrund von Kompatibilitätsproblemen zwischen den automatisch generierten AXI-Strukturen und den bestehenden I2S-Komponenten nicht umgesetzt werden.

Insgesamt zeigen beide Arbeiten komplementäre Lösungswege auf. Die Mikrocontroller-Variante punktet durch ihre Einfachheit, Offenheit und geringe Einstiegshürden, während die FPGA-basierte Lösung eine leistungsstarke und skalierbare Architektur für komplexe Anwendungen bereitstellt. Beide Umsetzungen verdeutlichen unterschiedliche Strategien zur Realisierung digitaler Filter und bieten eine fundierte Grundlage für zukünftige Lehr-, Forschungs- oder Entwicklungsprojekte.

18 Reflexion

Während der Bearbeitung der Arbeit traten mehrere unerwartete Herausforderungen auf, die zu wertvollen Lernerfahrungen führten und die Bedeutung praxisnaher Umsetzung deutlich machten.

Ein wesentlicher Rückschlag betraf die geplante Echtzeitfilterung von Audiosignalen über Mikrofoneingänge mit MicroPython. Die Grundidee war es, eine einfache, interpretierbare Umgebung zur Signalverarbeitung bereitzustellen. In der praktischen Umsetzung stellte sich jedoch heraus, dass kein passender Treiber für den Audio-Codec (ES8388) in MicroPython verfügbar war. Aufgrund fehlender Vorkenntnisse in der Treiberentwicklung und begrenzter Zeit war es nicht möglich, den Codec in MicroPython in Betrieb zu nehmen. Somit konnte die geplante Mikrofonverarbeitung in dieser Umgebung nicht umgesetzt werden. Diese Einschränkung verdeutlicht, wie wichtig ein direkter Zugriff auf die Hardware ist und wo die Grenzen von stark vereinfachten Programmiersprachen wie MicroPython bei hardwarenahen Anwendungen liegen.

Ein weiterer Reflexionspunkt betrifft die unerwartet aufwendige WAV-Dateiverarbeitung. Es wurde ursprünglich davon ausgegangen, dass der WAV-Header der Eingabedatei einfach übernommen werden könne. In der Praxis stellte sich jedoch heraus, dass ein vollständig neuer Header generiert werden musste, da bestimmte Felder (wie Dateigröße, Datenlänge und Subchunks) dynamisch angepasst werden müssen. Dies erforderte eine tiefere Auseinandersetzung mit dem WAV-Dateiformat und führte zu einem deutlich längeren und komplexeren Codeabschnitt als geplant. Gleichzeitig bot dieser Teil der Arbeit jedoch auch die Möglichkeit, sich intensiv mit binärer Datenverarbeitung und Dateistrukturen auseinanderzusetzen.

19 Schlussbetrachtung

Im Rahmen dieser Bachelorarbeit wurde die vollständige Implementierung und Evaluierung digitaler Biquad-Filter auf einem ressourcenbeschränkten Embedded-System, dem Lyrat V4.3 erfolgreich durchgeführt. Ziel war es, grundlegende Kenntnisse der digitalen Signalverarbeitung, insbesondere der digitalen Filtertechnik, praxisnah anzuwenden und auf reale Audioverarbeitungssysteme zu übertragen.

Ausgehend von einer fundierten theoretischen Auseinandersetzung mit den Eigenschaften, Strukturen und Entwurfsverfahren digitaler Biquads wurden praxisrelevante Filter in Python entworfen und analysiert. Die Implementierung auf Mikrocontroller-Ebene erfolgte sowohl in der Arduino-Umgebung als auch in MicroPython, wobei verschiedene Filterstrukturen (Direktform 1, Direktform 2, transponierte Direktform 2) zum Einsatz kamen.

Die durchgeführte Evaluierung zeigt, dass die Arduino-Umgebung deutlich überlegen ist, was Verarbeitungszeit, Echtzeitfähigkeit und praktische Anwendbarkeit betrifft. Während MicroPython sich gut für das prototypische Testen eignet, ist sie für leistungsaufwendige Audiosignalverarbeitung in Echtzeit nicht geeignet. Die TDF2-Struktur erwies sich als die stabilste und effizienteste Form der Filterumsetzung auf Mikrocontrollern. Auch die erfolgreiche Realisierung eines Kaskadenfilters sechster Ordnung demonstrierte die Skalierbarkeit des Konzepts ohne signifikanten Verlust an Performance.

Mit dieser Arbeit wurde gezeigt, dass sich anspruchsvolle digitale Signalverarbeitung auch auf leistungsschwacher Embedded-Hardware effektiv realisieren lässt, vorausgesetzt, Strukturwahl, Implementierung und Filterdesign sind sorgfältig aufeinander abgestimmt. Durch den konsequenten Bezug zur Praxis, kombiniert mit methodischem Vorgehen und objektiver Bewertung, leistet diese Arbeit einen Beitrag zur anwendungsorientierten Vermittlung digitaler Filtertechnik im Bereich der Mikrocontroller und Open-Scource.

20 Ausblick

Die im Rahmen dieser Arbeit entwickelte Implementierung digitaler Biquad-Filter auf Embedded-System bildet eine solide Grundlage für weiterführende Arbeiten in der digitalen Signalverarbeitung. Im nächsten Schritt bietet sich insbesondere die Erweiterung auf FIR-Filter (Finite Impulse Response) an. Diese stellen eine numerisch stabile Alternative zu IIR-Filtern dar und eignen sich durch ihre lineare Phasenlage besonders für Anwendungen in der Audiotechnik.

Darüber hinaus ließe sich die theoretische Basis deutlich vertiefen, etwa durch Inhalte aus dem Masterstudium wie Multiraten-Systeme, Filterbänke, Spektralschätzverfahren oder adaptive Filteralgorithmen. Eine solche Erweiterung der Theorie würde nicht nur eine umfangreichere Analyse ermöglichen, sondern auch den Übergang zu komplexeren digitalen Signalprozessor-Systemen vorbereiten.

Ein langfristiger Entwicklungspfad liegt schließlich in der Integration analoger Filterstrukturen in integrierter Form, durch den Entwurf und die Simulation analoger Hochfrequenzfilter als ASICs oder auf FPGA-Basis mit analogen Schnittstellen. Die Verbindung der digitalen Entwurfsumgebung mit einer realen Hardwareimplementierung auf analoger Ebene würde die Brücke zwischen der rein digitalen Signalverarbeitung und der physikalischen Signalwelt schlagen und ein tiefes Verständnis für die Systemintegration im Bereich des Analog-Mixed-Signal-Designs fördern.